Lab 10: More Generative Recursion, and a Pinch of Accumulators

• Work in Pairs
• Change roles often
• Follow the design recipes (for structural and generative recursion, and abstraction)

Warm-up: A Couple Circles and Several Spirals

Here's a bit of setup code:

     (require 2htdp/image)
     (require 2htdp/universe)

     ;; Constants
     (define WIDTH 300)
     (define HEIGHT 160)
     (define MT (empty-scene WIDTH HEIGHT))

     ;; next-size : Number -> Number
     (define (next-size s)
       (/ s 2))
        

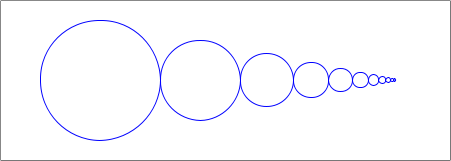
And here's our target image for the first function:

Note that the circles get smaller as they move to the right.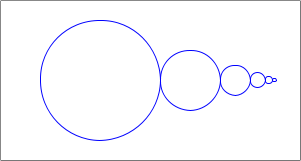

1. Design the function circles that takes two numbers, x and size, and a Scene scn.

   If size is less-than or equal to 2, then your function returns the scn unchanged (base case). Otherwise, your function should place a circle in the Scene that results from a recursive call to circles with x shifted by (+ size (next-size size)), a new size of (next-size size), and using the original Scene.

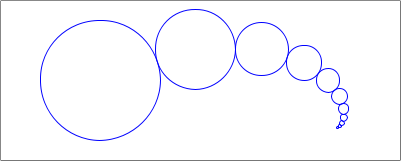
1. Adjust next-size so that it divides by 3/2 (or something a bit smaller), instead of 2.

   Modify WIDTH so you get something like the image below.

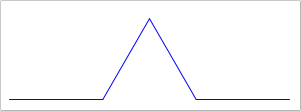
1. Now we create a similar function spiral, that takes four numbers and a Scene. In addition to x and size, the function also takes y and ang, which represent the center y coordinate of a circle, and the current angle (in radians).

   Now in your recursive call to spiral, you must update x and y based on your expert knowledge of trigonometry:

   next-x = x + (size+nextsize) * cos(ang)
   next-y = y + (size+nextsize) * sin(ang)

   And also add to the ang, something like (/ pi 10), with a starting angle of (/ pi -10) should give you something like the image below.

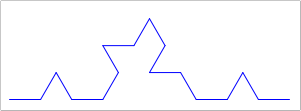
1. Modify the various parameters to your function to get interesting results.

   For example, if you modify the function to be structurally recursive (using sub1 instead of next-size), and draw the same size circles each time (be sure you terminate!), you might get something like the image below.

A Generative Fractal

Now that we've refreshed your trig senses, lets do a few generative fractals. First up is a simple "tree" fractal.

Here's some helper code to get you started:

          ;; put-line : Number Number Number Number String Scene -> Scene
          ;; Put a line in the scene starting at (x,y) len distance in the given direction
          ;;   with the given color
          (define (put-line x y ang len color scn)
            (place-image (line (* (cos ang) len)
                               (* (sin ang) len) color)
                         (+ x (* (cos ang) (/ len 2)))
                         (+ y (* (sin ang) (/ len 2))) scn))          
        

1. Design the function tree, that takes four numbers, x, y, ang, and len, and draws a tree into a given Scene.

   If the length is less than 3, then the function just puts a line at x/y/ang/len of some color (say green?) into the scene.

   Otherwise the function puts a brown line at x/y/ang/len, and recursivaly calls itself twice: once with x/y placed one third up the trunk at an angle off to the left, and another with x/y placed two thirds up the trunk at an angle off to the right. The length should be cut in half... altogether something like:

   next-x = x + len/3 * cos(ang)
   next-y = y + len/3 * sin(ang)
   next-ang = ang + pi/3
   next-len = len/2
   

   And the same for ang - pi/3, at 2*len/3 away.

   You should be able to modify the parameters to get various images such as the following... I did pi/6, and only cut the length in half.

Challenge: Koch Style Fractal

1. Similar to the tree fractal, we can do interesting things by changing recursive calls. The Koch snowflake is a rather cool recursive fractal.

   Design the function koch that takes the same arguments as tree, with an additional iter parameter that tracks the number of iterations left.

   For each iteration you cut the line into three pieces and make four recursive calls. The key is that you only put a line when the number of iterations are up (i.e., zero)

   The images below show the first 4 iterations and a more elaborate version (bigger, with 6 iterations), of a "snowflake" variation that I think looks pretty cool. See if you can emulate it.