CS7380 F10: Possible Errata and Clarifications
Here we list possible errata in the readings. In general these may not be confirmed with the author, hence we call them “possible” errata.
We also list some clarifications for possibly tricky sections.
Kortenkamp
- Top of page 53: “collinear” should be “concurrent”.
- Page 75: eq. 6.1 should be
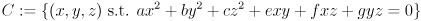 .
. - Page 75: eq. 6.2 should be
 .
. - Middle of page 77: “
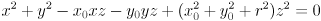 ” should be
” should be 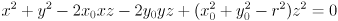 .
.
Bloomenthal and Rokne
- Bottom of page 6: “
 ” should be
” should be  .
. - Tottom of page 12: “
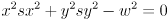 ” should be
” should be 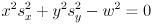 .
. - Top of page 13: “
 ” should be
” should be 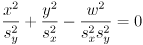 .
.
Shoemake
- Page 246, first paragraph: “position” should be “orientation”, i.e. a tumbling brick both translates and rotates in general; Euler’s rotation theorem only deals with rotation, not translation. Chasle’s theorem deals with both.
- Page 248, top right: the expression “
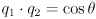 ” may be confusing. Here,
” may be confusing. Here, 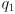 and
and  are quaternions, say
are quaternions, say 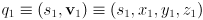 and similarly for
and similarly for  . However, for the purposes of taking the dot product
. However, for the purposes of taking the dot product  , they are temporarily considered simply 4-dimensional vectors:
, they are temporarily considered simply 4-dimensional vectors:  .
. - Page 248, second from last paragraph. An excerpt from the referenced book by Misner et al should shed more light on the idea of “entanglements” as used here.
- Page 249, figure “constructing a point for tangent”: the lower-left symbol in the figure may be hard to read; it should be “
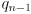 ”.
”. - Page 249, lower right: in the formula for
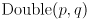
 and
and 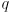 are quaternions but temporarily considered as vectors to evaluate the dot product
are quaternions but temporarily considered as vectors to evaluate the dot product 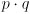 , just as was done for
, just as was done for 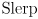 on p. 248.
on p. 248.
Grassia
- Page 6: “
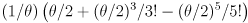 ” should be
” should be 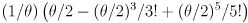 , and similar for all the other expansions of
, and similar for all the other expansions of 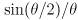 on the page.
on the page.
Selig
- Page 60, bottom: every
 term in the equations for
term in the equations for  should be negative
should be negative
Smith and Cheeseman
- Page 13: the first figure in section 4 is actually figure 5 in the paper, not figure 1 as it is labeled.
- Page 16: the third equation in equation group (14) should be
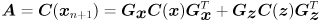 .
.
Zunino
- Page 34, bottom: change
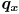 to
to 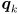 , and change "yielding
, and change "yielding  to
to 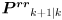 .
.
Bradski and Kaehler
- Page 164, last paragraph before start of section “Affine Transform”: change “a perspective transform can turn a rectangle into a trapezoid” to “a perspective transform can turn a rectangle into any quadrilateral”.
- Page 164, last line of second footnote: delete the word “orthogonal”.
- Page 165, figure 6–13: change “trapezoids” to “arbitrary quadrilaterals”.
- Page 167, footnote: change “trapezoid” to “arbitrary quadrilateral”.
- Page 317—318: the description of Harris corners, starting with the last paragraph on p. 317 and continuing for the first three paragraphs of p. 318, is unnecessarily confusing, and possibly erroneous. The wikipedia entry for Harris corners is much better (and start by reading the section on the Moravec corner dectector, which is the origin of the idea, and quite easy to understand). In fact, Harris corners do not use the Hessian matrix of second derivatives. The actual Harris algorithm is (1) calculate the
 matrix
matrix 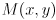 for each pixel
for each pixel  according to the equation at the top of p. 318 (note that in this equation
according to the equation at the top of p. 318 (note that in this equation 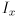 and
and  are the first derivatives of the image in the horizontal resp. vertical directions) and then (2) classify pixel
are the first derivatives of the image in the horizontal resp. vertical directions) and then (2) classify pixel  as a corner iff both eigenvalues (there will be two because
as a corner iff both eigenvalues (there will be two because 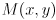 is
is  ) of
) of 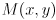 are “relatively large”. Harris suggested an approximation to this condition based on the determinant and trace of
are “relatively large”. Harris suggested an approximation to this condition based on the determinant and trace of 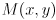 which saves a little computation vs actually computing the eigenvalues, but later Shi and Tomasi pointed out that it gives better results to actually compute the eigenvalues and verify that the smaller of the two is greater than some threshold.
which saves a little computation vs actually computing the eigenvalues, but later Shi and Tomasi pointed out that it gives better results to actually compute the eigenvalues and verify that the smaller of the two is greater than some threshold. - Page 329, top paragraph: replace both instances of “eigenvectors” with “eigenvalues”.
- Page 357: the second equation actually displays the transpose of
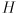 .
. - Page 371—373: Note that in the equations on these pages, lower-case variables such as
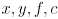 are in units of pixels, and upper-case variables such as
are in units of pixels, and upper-case variables such as 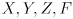 are in physical units, e.g. millimeters (any choice of physical units works as long as it is used consistently).
are in physical units, e.g. millimeters (any choice of physical units works as long as it is used consistently). - Page 373: in the second paragraph,
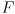 is the actual focal length in physical units (e.g. millimeters), and
is the actual focal length in physical units (e.g. millimeters), and 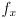 and
and 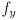 are effective horizontal and vertical focal lenghths in pixels. These differ only when the pixels are not actually square, i.e. when
are effective horizontal and vertical focal lenghths in pixels. These differ only when the pixels are not actually square, i.e. when  . In practice, despite what the book says, nowadays most cameras have square pixels, even cheap ones. Also, it is usually possible to get accurate specifications from the camera manufacturer of the designed values of
. In practice, despite what the book says, nowadays most cameras have square pixels, even cheap ones. Also, it is usually possible to get accurate specifications from the camera manufacturer of the designed values of 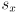 and
and 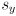 . The designed focal length
. The designed focal length 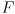 is also often specified, but the actual as-built value may differ somewhat.
is also often specified, but the actual as-built value may differ somewhat. - Page 376: the lower two equations on the page should be
 and
and  . Also, note that all equations on this page are given without derivation or detailed explanation; we’ll just take them at face value. The quantity
. Also, note that all equations on this page are given without derivation or detailed explanation; we’ll just take them at face value. The quantity 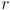 appearing in the equations is defined as the radial distance of the pixel
appearing in the equations is defined as the radial distance of the pixel  from the optical center
from the optical center  :
: 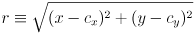 .
. - Page 380: replace the equation
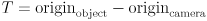 with
with  , and note that
, and note that 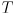 is calculated in object frame coordinates. This is fairly nonstandard, in particular note that the
is calculated in object frame coordinates. This is fairly nonstandard, in particular note that the 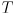 vector here is not the same as the
vector here is not the same as the  vector used later in the chapter (starting on p. 386). The
vector used later in the chapter (starting on p. 386). The 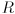 matrix is the same though. See further discussion below on a similar issue with the
matrix is the same though. See further discussion below on a similar issue with the 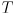 vector on p. 422—423.
vector on p. 422—423. - Page 381: “intrinsic corrections” and “intrinsics matrix”, terms used in the first and second paragraph, seem to not have been previously defined. Here, “intrinsic corrections” refers to both the pinhole model of the camera (equation at the top of p. 374), which is defined by four parameters
 , combined with the radial and tangential lens distortion models (equations on p. 376), which are defined by five parameters
, combined with the radial and tangential lens distortion models (equations on p. 376), which are defined by five parameters 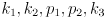 . Perhaps confusingly, “intrinsics matrix” refers only to the matrix
. Perhaps confusingly, “intrinsics matrix” refers only to the matrix  defined at the top of p. 374, i.e. the pinhole camera model. The discussion of the required number of equations on p. 381 mostly ignores the distortion parameters. Fortunately, the discussion is repeated in more detail, including the distortion parameters, on p. 388.
defined at the top of p. 374, i.e. the pinhole camera model. The discussion of the required number of equations on p. 381 mostly ignores the distortion parameters. Fortunately, the discussion is repeated in more detail, including the distortion parameters, on p. 388. - Page 385: note that the point
 is measured in physical units (e.g. millimeters) in a coordinate frame
is measured in physical units (e.g. millimeters) in a coordinate frame 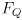 fixed to the moving object (i.e. the chessboard). Thus, if the chessboard has square cells of side length
fixed to the moving object (i.e. the chessboard). Thus, if the chessboard has square cells of side length 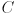 millimeters, its corners would have coordinates of the form
millimeters, its corners would have coordinates of the form  for integers
for integers  , assuming the chessboard is aligned so that one corner is at the origin of
, assuming the chessboard is aligned so that one corner is at the origin of 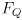 , that the
, that the  axis of
axis of 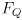 is normal to the plane of the chessboard, and that the
is normal to the plane of the chessboard, and that the 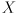 and
and 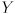 axes are aligned with the rows and columns of the chessboard. The point
axes are aligned with the rows and columns of the chessboard. The point  is in units of pixels in the image plane.
is in units of pixels in the image plane. - Page 386: in the sentence before the final equation on the page, replace
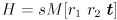 with
with 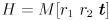 .
. - Page 390: delete the final transpose at the upper right of the third displayed equation on the page (i.e. the one beginning
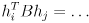 ).
). Page 391: while technically correct, the block of equations at the top of the page is unnecessarily complicated (this appears to be an artifact of translating the original equations from Zhang’s paper, which handles a slightly more general case). Note that here 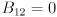 . Using that fact, and also substituting in the expressions in
. Using that fact, and also substituting in the expressions in  variables for the derived quantities
variables for the derived quantities 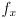 and
and 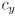 in the third and fifth equations, respectively, gives the following simpler set of equations:
in the third and fifth equations, respectively, gives the following simpler set of equations:
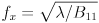

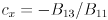
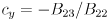
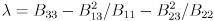 .
.
Also, the introduction of this particular 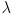 is not explained. It comes from the fact that if
is not explained. It comes from the fact that if 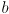 is a solution to the equation at the bottom of p. 390, then so is any scalar multiple of
is a solution to the equation at the bottom of p. 390, then so is any scalar multiple of 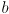 . Thus, the returned solution
. Thus, the returned solution 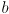 is actually multiplied by some unknown scalar factor
is actually multiplied by some unknown scalar factor 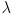 . Fortunately, here
. Fortunately, here 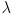 can be recovered by the above equation.
can be recovered by the above equation.- Page 391: in the second block of equations on the page, note that
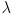 is not necessarily the same
is not necessarily the same 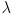 as in the first block of equations on the page.
as in the first block of equations on the page. - Page 391, bottom: the final expression for
 has a typo—rather than depending on
has a typo—rather than depending on  ,
,  depends on
depends on 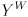 . Also, it is never explicitly stated, but the coordinates
. Also, it is never explicitly stated, but the coordinates 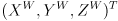 are produced by multiplying a point in object frame
are produced by multiplying a point in object frame 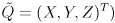 by the now-reconstructed extrinsic transformation matrix
by the now-reconstructed extrinsic transformation matrix 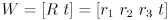 :
:

- Page 403, top paragraph: replace the phrase “your use of the jacobian function” with “your use of the cvRodrigues2 function”.
- Page 422, third paragraph: replace “We begin by considering the relationship between
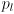 and
and 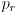 ” with "We begin by considering the relationship between
” with "We begin by considering the relationship between  and
and 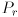 .
. - Pages 422—423: Note that the definition of the translation vector
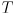 used in the section “Essential matrix math” is different from that used later in the chapter. However, this is ok, because each usage is self-consistent. The usage on 422—423 is relatively non-standard, and is similar to that on p. 380 (see above):
used in the section “Essential matrix math” is different from that used later in the chapter. However, this is ok, because each usage is self-consistent. The usage on 422—423 is relatively non-standard, and is similar to that on p. 380 (see above): 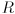 is an orthonormal basis for the left camera frame in the right camera frame (as would be typical for defining a rigid transform, as we are doing, from left camera coordinates to right camera coordinates), but (this is the nonstandard part) here
is an orthonormal basis for the left camera frame in the right camera frame (as would be typical for defining a rigid transform, as we are doing, from left camera coordinates to right camera coordinates), but (this is the nonstandard part) here 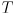 is the location of the right camera in the left camera frame; normally (i.e. as when forming the right column of a homogenous transformation matrix taking left camera coordinates to right camera coordinates) the translation vector would simply be the location of the left camera in the right camera frame.
is the location of the right camera in the left camera frame; normally (i.e. as when forming the right column of a homogenous transformation matrix taking left camera coordinates to right camera coordinates) the translation vector would simply be the location of the left camera in the right camera frame.
- Page 422, second from last paragraph: replace “all possible points
 through…” with “all possible points
through…” with “all possible points  on a plane through…”.
on a plane through…”. - Page 422, last paragraph: replace
 and
and 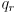 with
with 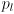 and
and 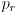 .
. - Page 422, first footnote: the second mention of
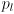 and
and 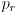 in the sentence should be replaced by
in the sentence should be replaced by  and
and 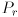 .
. - Page 424, top paragraph: replace all instances of
 with
with  , and replace “(the pixel coordinate)” with “(the camera frame coordinate)”.
, and replace “(the pixel coordinate)” with “(the camera frame coordinate)”. - Page 425, footnote: the description of the RANSAC algorithm is really LMedS and vice versa.
- Page 427, second paragraph: The first
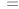 in
in  should be replaced by
should be replaced by  .
. Page 428, first footnote: replace the existing text with “Let’s be careful about what these terms mean:  and
and 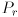 denote the locations of the 3D point
denote the locations of the 3D point  in the coordinate system of the left and right cameras, respectively.
in the coordinate system of the left and right cameras, respectively.  itself is in an object-relative coordinate frame
itself is in an object-relative coordinate frame 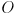 s.t.
s.t. 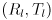 and
and 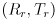 are rigid transforms that take coordinates in
are rigid transforms that take coordinates in 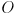 to the left resp. right camera frame.
to the left resp. right camera frame.  is a rigid transform that takes coordinates in the left camera frame to the right camera frame;
is a rigid transform that takes coordinates in the left camera frame to the right camera frame;  thus encodes the pose of the left camera with respect to the right.”
thus encodes the pose of the left camera with respect to the right.”
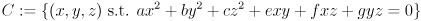 .
. .
.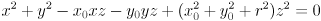 ” should be
” should be 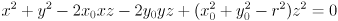 .
.![]() . Using that fact, and also substituting in the expressions in
. Using that fact, and also substituting in the expressions in ![]() variables for the derived quantities
variables for the derived quantities ![]() and
and ![]() in the third and fifth equations, respectively, gives the following simpler set of equations:
in the third and fifth equations, respectively, gives the following simpler set of equations:![]()
![]()
![]()
![]()
![]() .
.
![]() and
and ![]() denote the locations of the 3D point
denote the locations of the 3D point ![]() in the coordinate system of the left and right cameras, respectively.
in the coordinate system of the left and right cameras, respectively. ![]() itself is in an object-relative coordinate frame
itself is in an object-relative coordinate frame ![]() s.t.
s.t. ![]() and
and ![]() are rigid transforms that take coordinates in
are rigid transforms that take coordinates in ![]() to the left resp. right camera frame.
to the left resp. right camera frame. ![]() is a rigid transform that takes coordinates in the left camera frame to the right camera frame;
is a rigid transform that takes coordinates in the left camera frame to the right camera frame; ![]() thus encodes the pose of the left camera with respect to the right.”
thus encodes the pose of the left camera with respect to the right.”