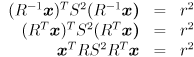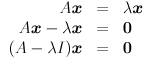CS7380 F10: HW3
DUE: 11:45am, Friday November 12
Worth: 10% of your final grade
The course policies page outlines academic honesty as applied to this course, including policies for working with other students on assignments. It also gives the rules for on-time homework submission.
Goals
- generate simple/fast 3D wireframe graphics using the pinhole camera model
- use OpenCV to track the 3D pose of a known object
- use OpenCV’s sparse pyramid Lucas-Kanade algorithm to track image features
- augment Lucas-Kanade tracking with a motion model and the Kalman Filter
- draw error ellipses for covariance matrices
Assignment
For this assignment you have the choice to do do either or both problems. Grading and turn-in details are given below.
- In this problem you will use OpenCV and a calibrated camera to track a known object in 3D. Specifically, you will use the OpenCV function
cvFindExtrinsicCameraParams2() to track the rigid transform that represents the pose of a chessboard calibration object relative to a camera. You will also use the theory of the pinhole camera model to draw simple 3D graphics which depict the chessboard and camera from an arbitrary external viewpoint.- Get a baseline program running which displays live images from your camera, as you did in HW2. You may use one of the example programs that were given with HW2. Again, aim for a resolution of
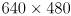 and about 10FPS. Get your printout of the chessboard calibration object and make arrangements so that you can move either it or the camera while keeping the chessboard flat and fully visible in the image. Your program should have a feature that pauses/unpauses the live video by hitting the spacebar, as the example programs
and about 10FPS. Get your printout of the chessboard calibration object and make arrangements so that you can move either it or the camera while keeping the chessboard flat and fully visible in the image. Your program should have a feature that pauses/unpauses the live video by hitting the spacebar, as the example programs cvdemo and cvundistort from HW2 do. - Undistort the live image using the calibration data you have already measured for your camera. If you’ll be coding in C++, you may use the
cvundistort example program; otherwise, use that as a reference to develop your own equivalent. Use these undistorted images for the remainder of the problem. - Define a right-handed 3D coordinate system
 that moves with the chessboard and which represents object frame. The origin of
that moves with the chessboard and which represents object frame. The origin of  is the lower left interior corner, the
is the lower left interior corner, the  axis points to the right across the columns, and the
axis points to the right across the columns, and the  axis points up across the rows.
axis points up across the rows. 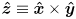 thus points out of the chessboard. Distance in
thus points out of the chessboard. Distance in  is measured in units of the chessboard pitch, so each of the
is measured in units of the chessboard pitch, so each of the 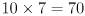 interior chessboard corners is defined by coordinates
interior chessboard corners is defined by coordinates 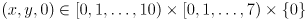 . For example, the coordinates of the lower left corner in
. For example, the coordinates of the lower left corner in  are
are 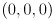 and those of the upper right corner are
and those of the upper right corner are 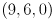 .
. - Define a second right-handed 3D coordinate system
 that moves with the camera and which represents camera frame. The origin of
that moves with the camera and which represents camera frame. The origin of  is the center of projection of the camera in the pinhole model,
is the center of projection of the camera in the pinhole model, 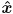 points towards the right side of the image,
points towards the right side of the image,  points down in the image, and
points down in the image, and 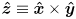 points straight forward along the optical axis. Distance in
points straight forward along the optical axis. Distance in  is also measured in units of the chessboard pitch.
is also measured in units of the chessboard pitch. - For every captured frame, use the OpenCV functions
cvFindChessboardCorners() and cvFindExtrinsicCameraParams2() to calculate a  3D rigid transformation matrix
3D rigid transformation matrix 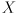 that takes points in
that takes points in  to points in
to points in  . Only calculate
. Only calculate 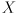 for frames where
for frames where cvFindChessboardCorners() returns nonzero, which indicates there is a high likelihood that the whole chessboard was detected correctly in the image. For frames where you calculate 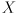 , draw a live reconstruction of the chessboard in magenta (
, draw a live reconstruction of the chessboard in magenta (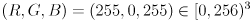 ) by calling
) by calling cvLine() to draw  lines in a grid covering the interior chessboard corners. (Draw nothing for frames where you did not calculate
lines in a grid covering the interior chessboard corners. (Draw nothing for frames where you did not calculate 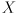 .)
.)
There are a few ways to interpret this. In particular, you could just use the pixel results of cvFindChessboardCorners() to get the image pixel locations of the endpoints of the lines, or you could calculate the 3D coordinates of those points in frame  , transform to
, transform to  , and then backproject into the image using the camera matrix. Because of what we are going to do next, please do the latter (*). Specifically, for each line (i) calculate the 3D endpoints
, and then backproject into the image using the camera matrix. Because of what we are going to do next, please do the latter (*). Specifically, for each line (i) calculate the 3D endpoints  in
in  , (ii) transform from
, (ii) transform from  to
to  by calculating
by calculating 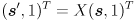 and similar for
and similar for 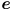 , (iii) backproject into the image by calculating
, (iii) backproject into the image by calculating 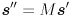 and similar for
and similar for 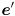 , where
, where 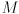 is the
is the 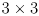 camera intrinsic matrix
camera intrinsic matrix
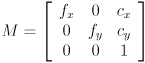 ,
,
and then perform the perspective division 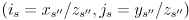 to get the pixel
to get the pixel 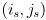 where
where 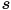 appears, and similar for
appears, and similar for 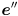 .
.
(*) The extent to which these two different approaches should give the same result depends precisely on how well the camera calibration models your actual camera, and on how accurate cvFindChessboardCorners() was.
On top of the drawing you made above, draw three colored line segments, all in 3D in the frame  : one from
: one from 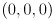 to
to 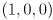 in red, another from
in red, another from 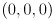 to
to 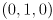 in green, and a third from
in green, and a third from 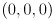 to
to  in blue. These represent the axis triad of
in blue. These represent the axis triad of  itself. Again, do this only for frames where you calculated
itself. Again, do this only for frames where you calculated 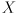 .
.
Your drawings both of the chessboard and of these axes should be updated for every new video frame. If you have implemented things correctly, it should look like they are virtually “stuck to” the chessboard as it moves around in 3D.Now introduce one more  rigid transform
rigid transform  into the projection chain. We will use this as a navigation transform to render a representation of both the chessboard and the camera from a simulated external viewpoint. This viewpoint will be modeled as if we had a second camera, with the same calibrated pinhole model as your actual camera, looking at the whole scene (chessboard and camera) from “outside”. Let
into the projection chain. We will use this as a navigation transform to render a representation of both the chessboard and the camera from a simulated external viewpoint. This viewpoint will be modeled as if we had a second camera, with the same calibrated pinhole model as your actual camera, looking at the whole scene (chessboard and camera) from “outside”. Let  be the camera frame of this simulated camera. Then
be the camera frame of this simulated camera. Then  is defined as the transform that takes points from
is defined as the transform that takes points from  to
to  , so the composite transform
, so the composite transform 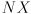 takes points from
takes points from  to
to  .
.
To make things interesting, you will handle keypresses that can change  , effectively allowing the simulated camera to “fly around”. We know that since
, effectively allowing the simulated camera to “fly around”. We know that since  is a 3D rigid body transform (i.e. a transform in
is a 3D rigid body transform (i.e. a transform in 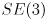 ) that it has six DoF, and that we can divide these up as three translations and three rotations. We will take the strategy of using six keys to control positive/negative translations along all three axes of
) that it has six DoF, and that we can divide these up as three translations and three rotations. We will take the strategy of using six keys to control positive/negative translations along all three axes of  , and four more keys to control positive/negative rotations about the
, and four more keys to control positive/negative rotations about the 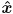 and
and  axes of
axes of  (we don’t allow the virtual camera to rotate around the
(we don’t allow the virtual camera to rotate around the 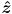 axis of
axis of  , this is a common design in part because this kind of “rolling” camera motion can be visually confusing).
, this is a common design in part because this kind of “rolling” camera motion can be visually confusing).
Set  to the identity transform initially. Implement keyboard handlers (i.e. using
to the identity transform initially. Implement keyboard handlers (i.e. using cvWaitKey(), or if you are using one of the CvBase implementations from HW2, just override handleKeyExt()) for the i and k keys that pitch the virtual camera by a rotation of 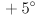 or
or 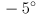 about the
about the 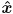 axis of
axis of  , respectively, and similarly make
, respectively, and similarly make j,l (that’s the letter j and the letter l keys) yaw by 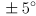 rotations about the
rotations about the  axis of
axis of  . Make
. Make e,d shift the virtual camera 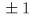 along the
along the  axis of
axis of  ,
, s,f shift by 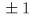 along the
along the 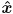 axis of
axis of  , and
, and a,z shift by 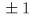 along the
along the 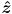 axis of
axis of  . Finally, make
. Finally, make r reset  to the identity transform. See below for an explanation of why we use these keys.
to the identity transform. See below for an explanation of why we use these keys.
Add drawing code for (i) an RGB axes triad for frame  (this is in addition to the one you already implemented for frame
(this is in addition to the one you already implemented for frame  ), and (ii) a very simple representation of the actual camera as a unit-altitude rectangular pyramid in yellow (
), and (ii) a very simple representation of the actual camera as a unit-altitude rectangular pyramid in yellow (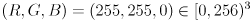 ), also in
), also in  , representing the horizontal and vertical FoV. I.e. the apex of this pyramid is
, representing the horizontal and vertical FoV. I.e. the apex of this pyramid is 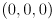 in
in  and the four base points are given by the four combinations
and the four base points are given by the four combinations
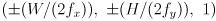
where 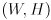 are the dimensions of your images in pixels (e.g.
are the dimensions of your images in pixels (e.g. 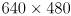 ).
).
Whenever  is not the identity matrix (i.e. whenever the virtual viewpoint does not correspond to the actual camera view), hide the actual captured images and make all your drawings on a white background. Conversely, whenever
is not the identity matrix (i.e. whenever the virtual viewpoint does not correspond to the actual camera view), hide the actual captured images and make all your drawings on a white background. Conversely, whenever  is identity, show the captured images instead of a white background, but hide your axis triad and pyramid in frame
is identity, show the captured images instead of a white background, but hide your axis triad and pyramid in frame  . As before, for all frames where you computed the transform
. As before, for all frames where you computed the transform 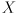 from
from  to
to  (i.e. whenever the chessboard was successfully detected, irrespective of
(i.e. whenever the chessboard was successfully detected, irrespective of  ), draw the axis triad in frame
), draw the axis triad in frame  and the reconstructed chessboard grid.
and the reconstructed chessboard grid.
Be sure that you can still change  while capture is paused.
while capture is paused.
- In this problem you will use OpenCV and an uncalibrated camera to track image features in 2D using sparse optical flow and a Kalman filter. Specifically, you will use
cvCalcOpticalFlowPyrLK() to track feature points, and you will use cvKalmanPredict() and cvKalmanCorrect() to incorporate a simple model of point motion.Starting with a basic program that displays images from your camera (aim for 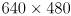 , 10FPS as usual), such as
, 10FPS as usual), such as cvdemo from HW2, add code that (i) adds and removes feature points where the user clicks the mouse on the image, displaying them as green dots, (ii) uses cvCalcOpticalFlowPyrLK() to track the points from frame to frame, and (iii) removes existing feature points either when they are clicked (at their current position, wherever it may be) or when their tracking fails or degrades below a threshold that you determine is reasonable.
Clearly, the provided lkdemo.c will be useful. Note that we will not need the ability to automatically initialize the feature points (cvGoodFeaturesToTrack()) or the “night mode” of lkdemo.
Your program should have a feature that pauses/unpauses the live video by hitting the spacebar, as the example programs like cvdemo from HW2 do. Make sure that adding and removing track points by clicking with the mouse works even when capture is paused.Define a  measurement covariance matrix
measurement covariance matrix
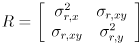 that models the uncertainty in the “measurement” of the location of any feature point returned by
that models the uncertainty in the “measurement” of the location of any feature point returned by cvCalcOpticalFlowPyrLK(). Though it is possible to estimate 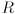 from the content of the image (see the end of the section on the Wikipedia entry for Harris corners), for our purposes we will take a simpler approach. We will set
from the content of the image (see the end of the section on the Wikipedia entry for Harris corners), for our purposes we will take a simpler approach. We will set 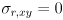 and
and  and
and 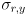 to constants. These are, respectively, the horizontal and vertical standard deviations of the error in the tracking results from
to constants. These are, respectively, the horizontal and vertical standard deviations of the error in the tracking results from cvCalcOpticalFlowPyrLK(); they are measured in pixels. Initialize 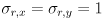 , and make the
, and make the e,d,s,f keys increment/decrement  (s-,f+) and
(s-,f+) and 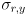 (e+,d-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console (i.e. with
(e+,d-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console (i.e. with printf() or cout or System.out.println()) whenever either is changed.- Add code that draws error ellipses in green for all of the points returned by
cvCalcOpticalFlowPyrLK(), which we will now call the measurements. To do this you will need to define a confidence limit  , which means that the actual location of each feature should be inside the corresponding ellipse with probability
, which means that the actual location of each feature should be inside the corresponding ellipse with probability  . Clearly, larger values of
. Clearly, larger values of  must correspond to larger ellipses. Handle
must correspond to larger ellipses. Handle 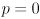 as a special case: simply don’t draw any ellipses. Initialize
as a special case: simply don’t draw any ellipses. Initialize 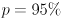 and make the
and make the a,z keys increment/decrement  by
by 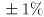 , respectively. Clamp
, respectively. Clamp  to the range
to the range  , and display its new value on the console whenever it is changed. (Be sure to also re-draw all the error ellipses whenever
, and display its new value on the console whenever it is changed. (Be sure to also re-draw all the error ellipses whenever  changes, even when capture is paused.)
changes, even when capture is paused.) Starting with the third frame received after a feature is added, it is possible to predict (or at least to make a reasonable guess about) the new location of the feature 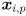 given its two previous locations
given its two previous locations 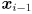 and
and 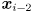 (here we are using
(here we are using  to index the sequence of video frames). There are various ways to do this depending on the assumptions we make about object motion. We will simply model the point to move with locally (locally in the temporal domain, that is) constant velocity in the image. We will also assume that the amount of time that passes between adjacent captured frames is constant. Thus, we initialize an estimate of the velocity of the feature from its first two observed locations as
to index the sequence of video frames). There are various ways to do this depending on the assumptions we make about object motion. We will simply model the point to move with locally (locally in the temporal domain, that is) constant velocity in the image. We will also assume that the amount of time that passes between adjacent captured frames is constant. Thus, we initialize an estimate of the velocity of the feature from its first two observed locations as 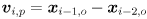 and we initialize an estimate of its position as
and we initialize an estimate of its position as 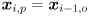 . The state of the feature is now the 4D vector
. The state of the feature is now the 4D vector 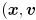 ). (Note that we only explicitly calculate the state by these equations to initialize it; later state updates will be completely determined by the Kalman filter.)
). (Note that we only explicitly calculate the state by these equations to initialize it; later state updates will be completely determined by the Kalman filter.)
Use cvKalmanPredict() to calculate 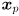 for every feature point that has been defined for at least 3 frames (because our model does not include any cross-correlation between features, you may use a separate
for every feature point that has been defined for at least 3 frames (because our model does not include any cross-correlation between features, you may use a separate CvKalman structure for each feature). Model the uncertainty in this prediction with a diagonal covariance matrix 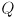 of the form
of the form
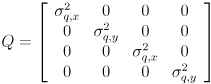
Initialize  (10 times larger than the initial setting of
(10 times larger than the initial setting of  and
and 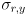 because we are significantly less certain of our simple model than of the measurements from
because we are significantly less certain of our simple model than of the measurements from cvCalcOpticalFlowPyrLK()), and make the i,k,j,l keys increment/decrement 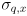 (j-,l+) and
(j-,l+) and 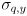 (i+,k-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console whenever either is changed.
(i+,k-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console whenever either is changed.
For every feature that has been present for at least 3 frames, draw the predicted location 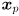 and its error ellipse, which is given by the upper-left
and its error ellipse, which is given by the upper-left 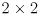 submatrix of
submatrix of 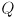 and the current value of the confidence limit
and the current value of the confidence limit  (use the same value of
(use the same value of  for all parts of this problem). Draw these in red.
for all parts of this problem). Draw these in red.For every feature that has been present for at least 3 frames, use cvKalmanCorrect() to combine the predicted state 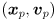 and the observation
and the observation 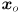 (the output of
(the output of cvCalcOpticalFlowPyrLK() for that feature) into an estimated state 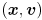 and
and  estimate covariance matrix
estimate covariance matrix 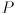 . Display the estimated location
. Display the estimated location 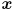 and its error ellipse (given by the upper left
and its error ellipse (given by the upper left 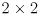 submatrix of
submatrix of 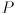 and the current value of
and the current value of  ) in blue, and use the predicted
) in blue, and use the predicted 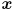 values to set the input
values to set the input prevFeatures for the next call to cvCalcOpticalFlowPyrLK().
Rationale for Keyboard Controls
Both problems require you to implement keypress handlers that increment/decrement quantities related to coordinate frame axes. For such purposes it might seem natural to use the arrow keys common on many keyboards. Unfortunately, the cvWaitKey() API that OpenCV provides to check for keyboard hits is fairly limited. In particular, it returns different values for the arrow keys on different platforms (OSX, Windows, Linux). Also, it is hard to detect modifier keys (shift, alt, ctrl, option, …) because they do not change the keycode emitted by other keys. (And OpenCV reports keypresses, including of modifier keys, but not releases, so you can’t even implement your own state tracking of the modifier keys.)
For these reasons, we chose arrangements of plain alphabetic keys which, in the standard QWERTY keyboard layout, approximate the up, down, left, right arrangement of the arrow keys. Specifically the groups e, d, s, f and i, k, j, l are used as two separate stand-ins for up, down, left, right. These groups also have the benefit that if you are a touch-typist you will typically have your index fingers on the f and j keys in “home” position (these are the keys with little nubs on them). There is some precedent for this design. Further, we can even extend our key groups into 3D: a, z and :, / (not letter keys, but still quite standard across platforms) can function as “in, out” keys for the right and left hand, respectively.
If you find these keybindings uncomfortable you may define other keyboard and mouse bindings in addition (your additional bindings may even be platform specific). E.g. you can implement a different mode that can be switched to by hitting some other key, or you can just use other non-overlapping keys, or even the mouse. But please make sure that by default the above keys have the intended effects so that we can easily run everyone’s code.
Drawing Error Ellipses
The connection between Gaussian distributions and ellipsoids is quite beautiful and draws together several topics we’ve studied in the course. We will develop a procedure now specifically to draw a 2D ellipse using cvEllipse() given three ingredients:
- the mean value
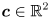 for a 2D Gaussian distribution
for a 2D Gaussian distribution - the
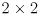 covariance matrix
covariance matrix  for that distribution (together these two things completely define the Gaussian, or Normal distribution, for which we use the notation
for that distribution (together these two things completely define the Gaussian, or Normal distribution, for which we use the notation 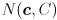 )
) - a scalar confidence limit
 , which gives the probability that the actual value
, which gives the probability that the actual value 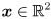 of the random variable modeled by the distribution will be found in the error ellipse
of the random variable modeled by the distribution will be found in the error ellipse 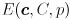 (this notation simply means the ellipse
(this notation simply means the ellipse 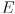 is some function of
is some function of  ,
,  , and
, and  ).
).
Informally,  gives the center of the ellipse,
gives the center of the ellipse,  gives its shape (how much it is squished in each of two orthogonal directions relative to a circle, which is a special case of an ellipse which is not squished at all) and also its orientation (how much it’s rotated compared to an ellipse in standard position, which is squished in exactly the
gives its shape (how much it is squished in each of two orthogonal directions relative to a circle, which is a special case of an ellipse which is not squished at all) and also its orientation (how much it’s rotated compared to an ellipse in standard position, which is squished in exactly the 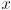 and
and 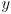 coordinate axes), and
coordinate axes), and  gives the scale of the ellipse: larger
gives the scale of the ellipse: larger  give larger ellipses.
give larger ellipses. 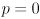 will give an ellipse that has degenerated to a single point; we do not allow
will give an ellipse that has degenerated to a single point; we do not allow  to reach
to reach 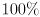 , but if we did, that would effectively correspond to an ellipse of infinite size.
, but if we did, that would effectively correspond to an ellipse of infinite size.
All of this extends in a mostly straightforward way to ellipsoids in arbitrary dimension (i.e. not just 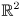 ). The details are given below
). The details are given below
We will first review the derivation and meaning of a particular form for the implicit equation for an ellipse. Then, we’ll show how to use elements of that equation to actually call cvEllipse() to draw an ellipse. Finally, we’ll show how to build such an equation from  ,
,  , and
, and  .
.
Implicit Equation for an Ellipse
Start with the equation for a circle centered at the origin with radius  :
:

The interpretation is that 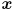 is on the circle iff the equation holds. Now we can squish (or stretch) the circle independently in the directions of the
is on the circle iff the equation holds. Now we can squish (or stretch) the circle independently in the directions of the 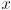 and
and 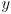 coordinate axes by first applying a nonuniform scale transform
coordinate axes by first applying a nonuniform scale transform
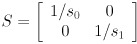
to every instance of 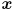 (the reason for using reciprocal scales will be given shortly), which gives us
(the reason for using reciprocal scales will be given shortly), which gives us

(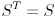 since
since  is diagonal). If we define
is diagonal). If we define 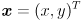 then this expands out to
then this expands out to
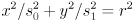
and from there it’s easy to calculate the horizontal and vertical radii 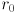 and
and 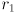 of the ellipse: for the horizontal case, plug in
of the ellipse: for the horizontal case, plug in 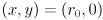
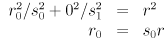
and similarly for the vertical case we get  . The scale factors, as we have defined them, are thus the “stretchings” of the radius of the original circle to make the ellipse radii. What happens if one of the scale factors, say
. The scale factors, as we have defined them, are thus the “stretchings” of the radius of the original circle to make the ellipse radii. What happens if one of the scale factors, say  , is zero? Then the corresponding radius is zero, but
, is zero? Then the corresponding radius is zero, but  will have an infinte entry. What happens if one of the diagonal elments of
will have an infinte entry. What happens if one of the diagonal elments of  is zero? Then the corresponding radius will be infinite. Both of these situations will have meaning below.
is zero? Then the corresponding radius will be infinite. Both of these situations will have meaning below.
So far we have an axis-aligned ellipse centered at the origin. The next step is to allow the ellipse to be rotated so that its major and minor axes do not necessarily have to align to the coordinate system 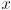 and
and 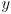 directions. We just need to multiply every instance of
directions. We just need to multiply every instance of 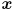 by an arbitrary 2D rotation transform
by an arbitrary 2D rotation transform
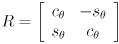
where 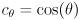 and
and 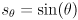 for an arbitrary CCW rotation
for an arbitrary CCW rotation 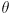 . We actually multiply by
. We actually multiply by 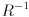 to have the effect of rotating back to standard position, where the stretching is done:
to have the effect of rotating back to standard position, where the stretching is done:
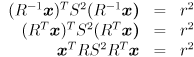
(using 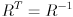 since
since 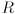 is orthogonal). By the way we have constructed this equation, the columns of
is orthogonal). By the way we have constructed this equation, the columns of 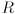 are unit vectors that point along the major and minor axes of the ellipse. Specifically, if
are unit vectors that point along the major and minor axes of the ellipse. Specifically, if 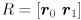 (naming the two columns of
(naming the two columns of 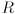 ) and
) and  then
then 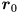 is a unit vector pointing along the major axis, which has radius
is a unit vector pointing along the major axis, which has radius 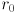 , and
, and 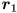 is a unit vector pointing along the minor axis, which has radius
is a unit vector pointing along the minor axis, which has radius 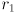 . “major” and “minor” are just swapped in that sentence if
. “major” and “minor” are just swapped in that sentence if 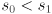 (and if
(and if 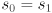 we have a circle, which is a special case of an ellipse).
we have a circle, which is a special case of an ellipse).
The final step is to allow the ellipse to be centered at some point other than the origin. Specifically, to center the ellipse at point  , just replace every instance of
, just replace every instance of 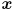 with
with 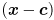 :
:
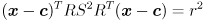
We can write this a little more compactly by defining 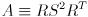 :
:
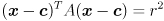
but note that we can’t just use any 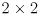 matrix for
matrix for  —it has to be decomposable into the form
—it has to be decomposable into the form 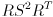 , where
, where 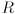 is orthogonal and
is orthogonal and  has non-negative entries on its main diagonal and is 0 elsewhere. It can be shown that these constraints are equivalent to saying that
has non-negative entries on its main diagonal and is 0 elsewhere. It can be shown that these constraints are equivalent to saying that  must be symmetric and positive semi-definite, i.e.
must be symmetric and positive semi-definite, i.e. 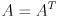 (symmetric) and
(symmetric) and  for any nonzero
for any nonzero 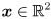 (positive semi-definite).
(positive semi-definite).
This is further equivalent to the following statement: if you are given an equation in the form
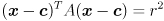
then this is the equation for an ellipse if and only if  can be decomposed into
can be decomposed into 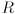 and
and  such that
such that 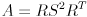 ,
, 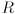 is orthogonal, and
is orthogonal, and  is positive semi-definite, which is possible if and only if
is positive semi-definite, which is possible if and only if  is symmetric and positive semi-definite. How can you check if
is symmetric and positive semi-definite. How can you check if  has these properties? And how can you actually perform the decomposition to get
has these properties? And how can you actually perform the decomposition to get 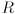 and
and  (you will need them to draw the ellipse)? It turns out that both questions can be answered by computing an eigendecomposition of
(you will need them to draw the ellipse)? It turns out that both questions can be answered by computing an eigendecomposition of  .
.
Any 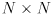 (i.e. square) matrix
(i.e. square) matrix  can be thought of as a function that transforms an non-zero input vector
can be thought of as a function that transforms an non-zero input vector 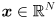 to some other vector
to some other vector  , by simple left multiplication:
, by simple left multiplication: 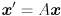 . In general, the “output” vector
. In general, the “output” vector  will not point in the same direction as
will not point in the same direction as 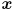 , nor will the length of the output vector be the same as the length of the input vector:
, nor will the length of the output vector be the same as the length of the input vector:  can both rotate and scale vectors. But it may happen that for some input vectors, the corresponding output vector is pointing in the same direction; i.e.,
can both rotate and scale vectors. But it may happen that for some input vectors, the corresponding output vector is pointing in the same direction; i.e.,  might have only a scaling effect on some vectors, so that
might have only a scaling effect on some vectors, so that 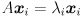 for some scalar
for some scalar 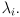 It is not too hard to convert this statement into a prescription for finding such scaling values
It is not too hard to convert this statement into a prescription for finding such scaling values 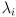 , which are called the eigenvalues of
, which are called the eigenvalues of  :
:
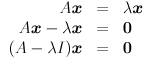
Where 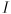 is the
is the 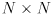 identity matrix. Since we specified that
identity matrix. Since we specified that 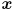 is non-zero, the only way this equation can hold is if the matrix
is non-zero, the only way this equation can hold is if the matrix 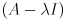 is not invertible, which is the same as saying its determinant is zero:
is not invertible, which is the same as saying its determinant is zero:
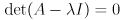
You may recall that there is a way to calculate determinants that boils down to finding the value of a degree- characteristic polynomial expression in terms of the entries in the matrix. Since
characteristic polynomial expression in terms of the entries in the matrix. Since  and
and 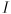 are constants, the only variable in this expression will be
are constants, the only variable in this expression will be 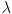 , and the roots of the polynomial will give the various eigenvalues
, and the roots of the polynomial will give the various eigenvalues 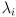 . In general there may be up to
. In general there may be up to  distinct
distinct 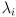 (there can be fewer because the characteristic polynomial can have multiple roots, in that case some
(there can be fewer because the characteristic polynomial can have multiple roots, in that case some 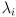 will have multiplicity greater than 1).
will have multiplicity greater than 1).
Given 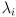 , the corresponding eigenvectors
, the corresponding eigenvectors 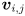 are a basis for the space of solutions to the specific equation
are a basis for the space of solutions to the specific equation 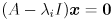 . This is a homogeneous system (right hand side
. This is a homogeneous system (right hand side 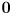 ) so it will, in general, have not just a single solution but an entire linear space of solutions.
) so it will, in general, have not just a single solution but an entire linear space of solutions.
We can finally define the eigendecomposition of  . Calculate all the eigenvalues
. Calculate all the eigenvalues 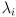 and corresponding eigenvectors
and corresponding eigenvectors 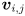 of
of  (there are good library routines available that will compute both the eigenvalues and eigenvectors for you, for arbitrary
(there are good library routines available that will compute both the eigenvalues and eigenvectors for you, for arbitrary  ). Note that if
). Note that if 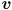 is an eigenvector then so is
is an eigenvector then so is  for any
for any 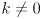 ; so we may normalize all the eigenvectors (this step is not strictly necessary, but assume we do so). If all the eigenvectors are linearly independent then it can be shown there are precisely
; so we may normalize all the eigenvectors (this step is not strictly necessary, but assume we do so). If all the eigenvectors are linearly independent then it can be shown there are precisely  of them and we may form an
of them and we may form an 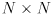 invertible matrix
invertible matrix 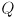 whose columns are simply the eigenvectors, which we can now index as
whose columns are simply the eigenvectors, which we can now index as 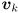 for
for 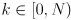 . If we re-index the corresponding eigenvalues as
. If we re-index the corresponding eigenvalues as  (allowing for multiple copies of eigenvalues with multiplicity greater than 1), then we can factor
(allowing for multiple copies of eigenvalues with multiplicity greater than 1), then we can factor  as
as
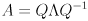
Where 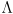 is an
is an 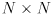 diagonal matrix with diagonal entries
diagonal matrix with diagonal entries  .
.
Note the similarity of this expression to the matrix in our ellipse equation.
In fact, it can be shown that  is symmetric and positive semi-definite exactly when all its eigenvalues are non-negative and
is symmetric and positive semi-definite exactly when all its eigenvalues are non-negative and 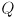 is orthogonal. This gives us not only a way to test if
is orthogonal. This gives us not only a way to test if  is suitable for use in the ellipse equation, but also a way to decompose it:
is suitable for use in the ellipse equation, but also a way to decompose it:
Compute the eigenvalues and eigenvectors of  (using
(using cvEigenVV() or, preferably, cvSVD() if you already know  is symmetric and positive semi-definite; for the
is symmetric and positive semi-definite; for the 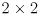 case it is actually possible to avoid use of these functions at all since the characteristic polynomial is just a quadratic, and easily solved by the quadratic equation, but the numerical methods will work for any dimension).
case it is actually possible to avoid use of these functions at all since the characteristic polynomial is just a quadratic, and easily solved by the quadratic equation, but the numerical methods will work for any dimension).
If you’re not sure if  was symmetric and positive semi-definite, check that the eigenvectors are linearly independent and that the eigenvalues are all positive.
was symmetric and positive semi-definite, check that the eigenvectors are linearly independent and that the eigenvalues are all positive.
Once  is found to be symmetric and positive semi-definite, just set
is found to be symmetric and positive semi-definite, just set 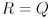 and
and 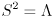 .
.
For the two dimensional case let the two eigenvalues be 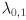 . Assume we’ve already verified that both are non-negative. Now we can easily find
. Assume we’ve already verified that both are non-negative. Now we can easily find 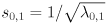 and
and 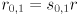 . NOTE: as we move on to covariance matrices below, will will find ourselves starting with an eigendecomposition of the inverse of
. NOTE: as we move on to covariance matrices below, will will find ourselves starting with an eigendecomposition of the inverse of  , so the scale factors will then be directly proportional to the square roots of the eigenvalues, not inversely proportional.
, so the scale factors will then be directly proportional to the square roots of the eigenvalues, not inversely proportional.
Drawing an Ellipse
cvEllipse() takes many parameters, but the geometry of the ellipse is effectively specified by just three: center, axes, and angle. Given an ellipse equation in the form
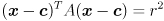
with  symmetric and positive definite, eigendecompose
symmetric and positive definite, eigendecompose  to get the rotation matrix
to get the rotation matrix 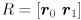 and the eigenvalues
and the eigenvalues 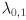 .
. center is just  .
. axes is a CvSize struct (for whatever reason) and can be constructed by calling cvSize(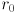 ,
, 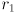 ), with the ellipse radii
), with the ellipse radii 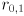 calculated from
calculated from 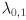 as described above.
as described above. angle is the CCW angle in degrees from the positive 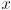 axis of the image coordinate frame to the axis of the ellipse corresponding to
axis of the image coordinate frame to the axis of the ellipse corresponding to 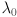 . Thus
. Thus angle is 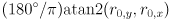 .
.
Building an Ellipse Equation from a Gaussian Distribution
We now make the connection to Gaussian distributions. Recall that given a 2D Gaussian distribution 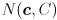 with mean value
with mean value  and covariance matrix
and covariance matrix  , and a confidence limit
, and a confidence limit  , we want to draw an ellipse such that a random variable drawn from
, we want to draw an ellipse such that a random variable drawn from 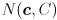 will be found inside the ellipse with probability
will be found inside the ellipse with probability  .
.
The definition of the Gaussian function gives the probability that any particular 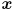 would be drawn:
would be drawn:
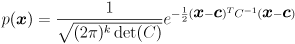
(Any covariance matrix  used in the definition of a Gaussian, as in this equation, must actually be positive definite, not just positive semi-definite. That ensures both that
used in the definition of a Gaussian, as in this equation, must actually be positive definite, not just positive semi-definite. That ensures both that 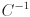 exists and that
exists and that 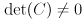 . The probability distribution associated with a covariance matrix that is only positive semi-definite is not strictly a Gaussian, however, it is still possible to draw an error ellipsoid for it. Our method for drawing ellipsoids allows this case; the ellipsoid will have one or more zero radii in the direction(s) corresponding to its zero eigenvalues.)
. The probability distribution associated with a covariance matrix that is only positive semi-definite is not strictly a Gaussian, however, it is still possible to draw an error ellipsoid for it. Our method for drawing ellipsoids allows this case; the ellipsoid will have one or more zero radii in the direction(s) corresponding to its zero eigenvalues.)
Note that the argument 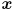 appears only in the exponent
appears only in the exponent
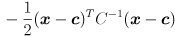
(look familiar?). Clearly, level sets of 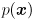 (sets of
(sets of 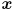 for which
for which 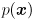 is constant) are equivalent to level sets of this expression. Furthermore, the maximum value of
is constant) are equivalent to level sets of this expression. Furthermore, the maximum value of 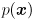 occurs at the maximum value of the exponent when
occurs at the maximum value of the exponent when 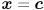 , and
, and 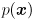 monotonically decreases in all directions as the distance
monotonically decreases in all directions as the distance 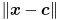 increases.
increases.
What all of this means is that there is some value 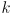 of the exponent for which any desired fraction
of the exponent for which any desired fraction 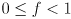 of the probability distribution is given by the
of the probability distribution is given by the 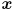 such that
such that

(i.e. 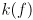 is some as-yet unspecified function of
is some as-yet unspecified function of 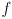 ).
). 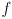 is determined directly from the confidence limit
is determined directly from the confidence limit  :
: 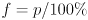 .
.
It can be shown that the covariance matrix  for any Gaussian is symmetric and positive definite. Thus, it is not necessary to check for these conditions when dealing with covariance matrices—you may assume them to be true. Furthermore, if
for any Gaussian is symmetric and positive definite. Thus, it is not necessary to check for these conditions when dealing with covariance matrices—you may assume them to be true. Furthermore, if 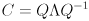 is the eigendecomposition of
is the eigendecomposition of  then the eigendecomposition of
then the eigendecomposition of 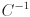 is easy to get:
is easy to get:

(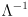 is easy to compute since the inverse of a diagonal matrix is trivially formed by taking the reciprocal of each entry on the diagonal.) This also shows that the inverse of a symmetric positive definite matrix is itself symmetric and positive definite. (If the matrix is only positive semi-definite, then replace the inverse with the pseudoinverse
is easy to compute since the inverse of a diagonal matrix is trivially formed by taking the reciprocal of each entry on the diagonal.) This also shows that the inverse of a symmetric positive definite matrix is itself symmetric and positive definite. (If the matrix is only positive semi-definite, then replace the inverse with the pseudoinverse 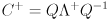 , which differs only in that
, which differs only in that  is formed by taking the reciprocal of each entry on the diagonal of
is formed by taking the reciprocal of each entry on the diagonal of 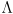 but with
but with 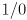 taken to be zero.)
taken to be zero.)
Now the connection to ellipses should be very clear: with 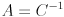 and
and 
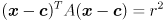
is the error ellipse of the distribution 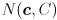 for the confidence limit
for the confidence limit  . The eigenvectors of
. The eigenvectors of  are the same as the eigenvectors of
are the same as the eigenvectors of  ; the eigenvalues of
; the eigenvalues of  are just the reciprocals of the eigenvalues
are just the reciprocals of the eigenvalues 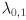 of
of  . The ellipse is centered at
. The ellipse is centered at  , has axis radii
, has axis radii 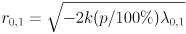 (here
(here 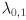 are the eigenvalues of
are the eigenvalues of  , so the ellipse radii are directly proportional to their square roots; note that a zero covariance matrix eigenvalue will correspond to a zero radius, and an infinite covariance matrix eigenvalue will correspond to an infinite radius), and the eigenvectors of
, so the ellipse radii are directly proportional to their square roots; note that a zero covariance matrix eigenvalue will correspond to a zero radius, and an infinite covariance matrix eigenvalue will correspond to an infinite radius), and the eigenvectors of  give the corresponding axis directions.
give the corresponding axis directions.
The final remaining piece of business is to determine the function 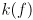 . The story is a little odd. It turns out that for the two dimensional case,
. The story is a little odd. It turns out that for the two dimensional case, 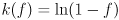 (this can be derived from the development in Appendix A of [1]). But for other dimensions it is not even possible in general to write down
(this can be derived from the development in Appendix A of [1]). But for other dimensions it is not even possible in general to write down 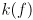 in closed form. Fortunately, the value of
in closed form. Fortunately, the value of 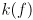 for any given
for any given 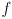 can be evaluated, in any dimension, to a high precision by a fast algorithm. The details are given in (e.g.) Numerical Recipes in C by Press et al.
can be evaluated, in any dimension, to a high precision by a fast algorithm. The details are given in (e.g.) Numerical Recipes in C by Press et al.
[1] Randall C. Smith, Peter Cheeseman, “On the Representation and Estimation of Spatial Uncertainty,” the International Journal of Robotics Research, Vol.5, No.4, Winter 1986. (This is an earlier version of the Smith and Cheeseman paper that we read in class.)
Ellipsoids in Higher Dimensions
All of the development so far generalizes trivially to ellipsoids, the arbitrary-dimensional generalization of ellipses. A Gaussian distribution in 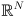 just has
just has 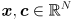 and an
and an 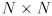 covariance matrix
covariance matrix  . The confidence limit
. The confidence limit  is always a scalar. The ellipse equation keeps the same form, but now the ellipsoid will have
is always a scalar. The ellipse equation keeps the same form, but now the ellipsoid will have  axes. For example, a 3D ellipsoid is shaped something like an American football that has been flattened a little.
axes. For example, a 3D ellipsoid is shaped something like an American football that has been flattened a little.
The only catch is the function 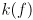 that determines the scale of the ellipsoid given
that determines the scale of the ellipsoid given 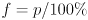 . As stated above, there is not a closed form expression for
. As stated above, there is not a closed form expression for 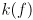 in general, but the required value can be computed by a fast algorithm.
in general, but the required value can be computed by a fast algorithm.
Finally, it is frequently desired to show the error ellipse (or 3D error ellipsoid) for a subset of the variables in a higher dimensional Gaussian distribution. This turns out to be quite easy: just strike out the rows and columns corresponding to the unneeded variables from the higher dimensional covariance matrix  to yield the required
to yield the required 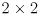 (or
(or 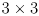 ) covariance matrix. Similarly strike out the unneeded entries in the mean value
) covariance matrix. Similarly strike out the unneeded entries in the mean value  , and evaluate
, and evaluate 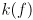 for the target dimension (2 or 3).
for the target dimension (2 or 3).
Turn In
Since both problems are coding work, you may work with a partner on this assignment. In fact, we encourage it. Follow the instructions on the assignments page to submit all your code.
Grading
100 points will be allocated according to how many problems you choose to complete. If you do both problems then we will grade each out of 100% and your score will be the maximum of the two.
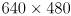 and about 10FPS. Get your printout of the chessboard calibration object and make arrangements so that you can move either it or the camera while keeping the chessboard flat and fully visible in the image. Your program should have a feature that pauses/unpauses the live video by hitting the spacebar, as the example programs
and about 10FPS. Get your printout of the chessboard calibration object and make arrangements so that you can move either it or the camera while keeping the chessboard flat and fully visible in the image. Your program should have a feature that pauses/unpauses the live video by hitting the spacebar, as the example programs  that moves with the chessboard and which represents object frame. The origin of
that moves with the chessboard and which represents object frame. The origin of  is the lower left interior corner, the
is the lower left interior corner, the 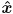 axis points to the right across the columns, and the
axis points to the right across the columns, and the  axis points up across the rows.
axis points up across the rows. 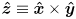 thus points out of the chessboard. Distance in
thus points out of the chessboard. Distance in  is measured in units of the chessboard pitch, so each of the
is measured in units of the chessboard pitch, so each of the 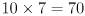 interior chessboard corners is defined by coordinates
interior chessboard corners is defined by coordinates 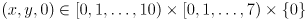 . For example, the coordinates of the lower left corner in
. For example, the coordinates of the lower left corner in  are
are 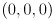 and those of the upper right corner are
and those of the upper right corner are 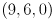 .
. that moves with the camera and which represents camera frame. The origin of
that moves with the camera and which represents camera frame. The origin of  is the center of projection of the camera in the pinhole model,
is the center of projection of the camera in the pinhole model, 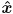 points towards the right side of the image,
points towards the right side of the image,  points down in the image, and
points down in the image, and 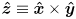 points straight forward along the optical axis. Distance in
points straight forward along the optical axis. Distance in  is also measured in units of the chessboard pitch.
is also measured in units of the chessboard pitch. 3D rigid transformation matrix
3D rigid transformation matrix 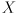 that takes points in
that takes points in  to points in
to points in  . Only calculate
. Only calculate 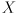 for frames where
for frames where 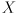 , draw a live reconstruction of the chessboard in magenta (
, draw a live reconstruction of the chessboard in magenta (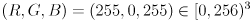 ) by calling
) by calling 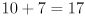 lines in a grid covering the interior chessboard corners. (Draw nothing for frames where you did not calculate
lines in a grid covering the interior chessboard corners. (Draw nothing for frames where you did not calculate 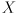 .)
.) , transform to
, transform to  , and then backproject into the image using the camera matrix. Because of what we are going to do next, please do the latter (*). Specifically, for each line (i) calculate the 3D endpoints
, and then backproject into the image using the camera matrix. Because of what we are going to do next, please do the latter (*). Specifically, for each line (i) calculate the 3D endpoints  in
in  , (ii) transform from
, (ii) transform from  to
to  by calculating
by calculating 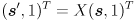 and similar for
and similar for 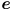 , (iii) backproject into the image by calculating
, (iii) backproject into the image by calculating 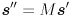 and similar for
and similar for 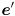 , where
, where 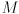 is the
is the  camera intrinsic matrix
camera intrinsic matrix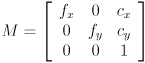 ,
,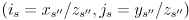 to get the pixel
to get the pixel 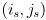 where
where 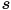 appears, and similar for
appears, and similar for 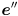 .
. : one from
: one from 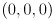 to
to 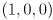 in red, another from
in red, another from 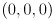 to
to 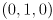 in green, and a third from
in green, and a third from 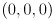 to
to  in blue. These represent the axis triad of
in blue. These represent the axis triad of  itself. Again, do this only for frames where you calculated
itself. Again, do this only for frames where you calculated 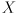 .
. rigid transform
rigid transform  into the projection chain. We will use this as a navigation transform to render a representation of both the chessboard and the camera from a simulated external viewpoint. This viewpoint will be modeled as if we had a second camera, with the same calibrated pinhole model as your actual camera, looking at the whole scene (chessboard and camera) from “outside”. Let
into the projection chain. We will use this as a navigation transform to render a representation of both the chessboard and the camera from a simulated external viewpoint. This viewpoint will be modeled as if we had a second camera, with the same calibrated pinhole model as your actual camera, looking at the whole scene (chessboard and camera) from “outside”. Let  be the camera frame of this simulated camera. Then
be the camera frame of this simulated camera. Then  is defined as the transform that takes points from
is defined as the transform that takes points from  to
to  , so the composite transform
, so the composite transform 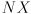 takes points from
takes points from  to
to  .
. , effectively allowing the simulated camera to “fly around”. We know that since
, effectively allowing the simulated camera to “fly around”. We know that since  is a 3D rigid body transform (i.e. a transform in
is a 3D rigid body transform (i.e. a transform in 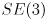 ) that it has six DoF, and that we can divide these up as three translations and three rotations. We will take the strategy of using six keys to control positive/negative translations along all three axes of
) that it has six DoF, and that we can divide these up as three translations and three rotations. We will take the strategy of using six keys to control positive/negative translations along all three axes of  , and four more keys to control positive/negative rotations about the
, and four more keys to control positive/negative rotations about the 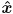 and
and  axes of
axes of  (we don’t allow the virtual camera to rotate around the
(we don’t allow the virtual camera to rotate around the 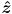 axis of
axis of  , this is a common design in part because this kind of “rolling” camera motion can be visually confusing).
, this is a common design in part because this kind of “rolling” camera motion can be visually confusing). to the identity transform initially. Implement keyboard handlers (i.e. using
to the identity transform initially. Implement keyboard handlers (i.e. using 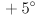 or
or 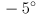 about the
about the 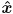 axis of
axis of  , respectively, and similarly make
, respectively, and similarly make 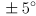 rotations about the
rotations about the  axis of
axis of  . Make
. Make 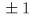 along the
along the  axis of
axis of  ,
, 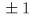 along the
along the 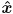 axis of
axis of  , and
, and 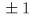 along the
along the 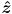 axis of
axis of  . Finally, make
. Finally, make  to the identity transform. See below for an explanation of why we use these keys.
to the identity transform. See below for an explanation of why we use these keys. (this is in addition to the one you already implemented for frame
(this is in addition to the one you already implemented for frame  ), and (ii) a very simple representation of the actual camera as a unit-altitude rectangular pyramid in yellow (
), and (ii) a very simple representation of the actual camera as a unit-altitude rectangular pyramid in yellow (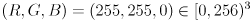 ), also in
), also in  , representing the horizontal and vertical FoV. I.e. the apex of this pyramid is
, representing the horizontal and vertical FoV. I.e. the apex of this pyramid is 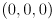 in
in  and the four base points are given by the four combinations
and the four base points are given by the four combinations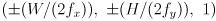
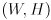 are the dimensions of your images in pixels (e.g.
are the dimensions of your images in pixels (e.g. 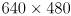 ).
). is not the identity matrix (i.e. whenever the virtual viewpoint does not correspond to the actual camera view), hide the actual captured images and make all your drawings on a white background. Conversely, whenever
is not the identity matrix (i.e. whenever the virtual viewpoint does not correspond to the actual camera view), hide the actual captured images and make all your drawings on a white background. Conversely, whenever  is identity, show the captured images instead of a white background, but hide your axis triad and pyramid in frame
is identity, show the captured images instead of a white background, but hide your axis triad and pyramid in frame  . As before, for all frames where you computed the transform
. As before, for all frames where you computed the transform 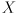 from
from  to
to  (i.e. whenever the chessboard was successfully detected, irrespective of
(i.e. whenever the chessboard was successfully detected, irrespective of  ), draw the axis triad in frame
), draw the axis triad in frame  and the reconstructed chessboard grid.
and the reconstructed chessboard grid. while capture is paused.
while capture is paused.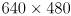 , 10FPS as usual), such as
, 10FPS as usual), such as  measurement covariance matrix
measurement covariance matrix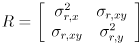
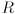 from the content of the image (see the end of the section on the Wikipedia entry for Harris corners), for our purposes we will take a simpler approach. We will set
from the content of the image (see the end of the section on the Wikipedia entry for Harris corners), for our purposes we will take a simpler approach. We will set 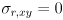 and
and  and
and 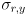 to constants. These are, respectively, the horizontal and vertical standard deviations of the error in the tracking results from
to constants. These are, respectively, the horizontal and vertical standard deviations of the error in the tracking results from 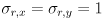 , and make the
, and make the  (s-,f+) and
(s-,f+) and 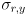 (e+,d-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console (i.e. with
(e+,d-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console (i.e. with  , which means that the actual location of each feature should be inside the corresponding ellipse with probability
, which means that the actual location of each feature should be inside the corresponding ellipse with probability  . Clearly, larger values of
. Clearly, larger values of  must correspond to larger ellipses. Handle
must correspond to larger ellipses. Handle 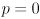 as a special case: simply don’t draw any ellipses. Initialize
as a special case: simply don’t draw any ellipses. Initialize 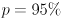 and make the
and make the  by
by 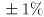 , respectively. Clamp
, respectively. Clamp  to the range
to the range  , and display its new value on the console whenever it is changed. (Be sure to also re-draw all the error ellipses whenever
, and display its new value on the console whenever it is changed. (Be sure to also re-draw all the error ellipses whenever  changes, even when capture is paused.)
changes, even when capture is paused.)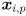 given its two previous locations
given its two previous locations 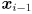 and
and 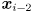 (here we are using
(here we are using  to index the sequence of video frames). There are various ways to do this depending on the assumptions we make about object motion. We will simply model the point to move with locally (locally in the temporal domain, that is) constant velocity in the image. We will also assume that the amount of time that passes between adjacent captured frames is constant. Thus, we initialize an estimate of the velocity of the feature from its first two observed locations as
to index the sequence of video frames). There are various ways to do this depending on the assumptions we make about object motion. We will simply model the point to move with locally (locally in the temporal domain, that is) constant velocity in the image. We will also assume that the amount of time that passes between adjacent captured frames is constant. Thus, we initialize an estimate of the velocity of the feature from its first two observed locations as 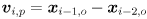 and we initialize an estimate of its position as
and we initialize an estimate of its position as 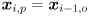 . The state of the feature is now the 4D vector
. The state of the feature is now the 4D vector 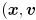 ). (Note that we only explicitly calculate the state by these equations to initialize it; later state updates will be completely determined by the Kalman filter.)
). (Note that we only explicitly calculate the state by these equations to initialize it; later state updates will be completely determined by the Kalman filter.)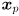 for every feature point that has been defined for at least 3 frames (because our model does not include any cross-correlation between features, you may use a separate
for every feature point that has been defined for at least 3 frames (because our model does not include any cross-correlation between features, you may use a separate 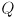 of the form
of the form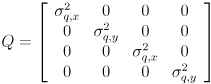
 (10 times larger than the initial setting of
(10 times larger than the initial setting of  and
and 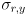 because we are significantly less certain of our simple model than of the measurements from
because we are significantly less certain of our simple model than of the measurements from 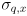 (j-,l+) and
(j-,l+) and 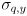 (i+,k-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console whenever either is changed.
(i+,k-) by 0.1. (See below for an explanation of why we use these keys.) Clamp the minimum value of each to 0.1 and display the new settings for both on the console whenever either is changed.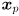 and its error ellipse, which is given by the upper-left
and its error ellipse, which is given by the upper-left 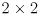 submatrix of
submatrix of 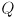 and the current value of the confidence limit
and the current value of the confidence limit  (use the same value of
(use the same value of  for all parts of this problem). Draw these in red.
for all parts of this problem). Draw these in red.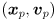 and the observation
and the observation 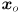 (the output of
(the output of 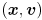 and
and  estimate covariance matrix
estimate covariance matrix 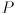 . Display the estimated location
. Display the estimated location 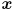 and its error ellipse (given by the upper left
and its error ellipse (given by the upper left 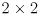 submatrix of
submatrix of 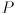 and the current value of
and the current value of  ) in blue, and use the predicted
) in blue, and use the predicted 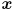 values to set the input
values to set the input