(in collaboration with Carrick Detweiler)
|
| kinematic chain simulation (in collaboration with Carrick Detweiler) |
This is the homepage for the 2012 Spring offering of CS5350 Applied Geometric Representation and Computation, a topics course at the College of Computer and Information Science at Northeastern University.
The course surveys practical techniques for representing geometric objects in two and three dimensions, for computing their motions and interactions, and for human interfaces to manipulate them. These techniques are useful not only in graphics, but also in robotics, computer vision, game design, geographic information systems, computer-aided design and manufacturing, spatial reasoning and planning, physical simulation, biomechanics, and the implementation of many types of human-computer interface.
Participation of Ph.D., M.S., and advanced undergraduates from a broad range of backgrounds is encouraged. No prior coursework in graphics or geometry is required. The course will require only basic skills in multivariable calculus, linear algebra, algorithm analysis, and programming. More details on prerequisites are given below.
We break the term into a set of one- and two-week units on different subtopics. To some extent, the focus of each unit and and the amount of time spent on it will be determined by the interests of the enrolled students. Units will be selected from the following topics:
 |
| [Kortenkamp 99] |
Two non-parallel lines in the plane intersect at one point. But consider rotating one of the lines—eventually, a parallel configuration is reached, and the intersection disappears. How would you handle this in software? What if some further construction depended on the intersection point? We will study a set of techniques that enable objects to move to “infinity” without any special-case code. An example system that has been built using these ideas is Kortenkamp’s Cinderella, which supports continuously editable ruler-and-compass style constructions like the one shown here.
 |
| [Peters] |
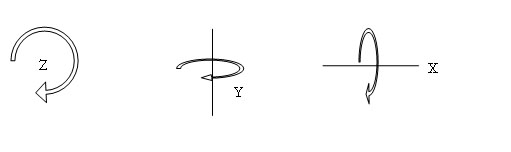
What is the fewest number of parameters sufficient to encode the 3D position and orientation of an arbitrary (asymmetric) rigid object? The answer is six; one way to further divide up these degrees of freedom is to allocate three for translation and three for rotation (relative to a fixed coordinate system). The space of all 3D translations is in fact 
, so no problem there, but the space of all 3D rotations is not —it is topologically different. This difference sometimes matters and sometimes can be ignored; we will study both cases and associated practical representations and algorithms, including unit quaternions, their exponential and logarithmic maps, Euler angles, and rotation matrices.
| |
| [Vona, Detweiler, Rus 06] |
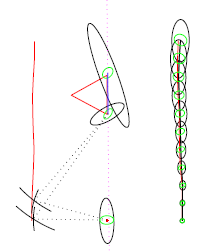
To a first approximation, your arm is a chain of joints alternating with rigid pieces—shoulder joint, upper arm, elbow joint, forearm, wrist joint, and hand. Say you are given a set of 3D coordinates at which your hand should be placed. How do you calculate the settings for the shoulder, elbow, and wrist joints which achieves this pose? This is a problem in inverse kinematics. We will study a modern, general-purpose algorithm for solving problems like this, not just for the human arm, but for a broad class of mechanisms including long chains as in the simulation pictured at right.
 |
| [Rikoski, Leonard, Newman 02] |
Given a set of measurements of the relative positions of different objects, or landmarks, each including a quantified amount of uncertainty, how can we best build a spatial map of them all? What if the relationship between two landmarks is later re-observed with more certainty? Or what if a previously unmeasured relationship is added? These questions have been intensely studied for the last 20 years in an area of research called Simultaneous Localization and Mapping (SLAM). We will study some of the original works that define this problem and that develop canonical solutions, as well as some modern applications.
 |
| [Calin and Roda] |
 |
| [NASA/JPL] |
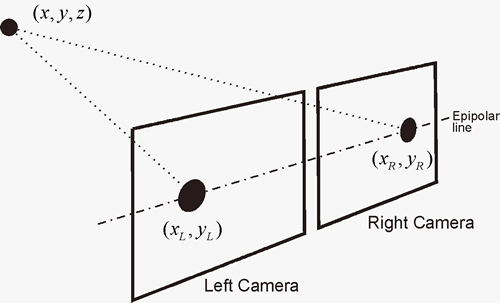
Clearly, a single image of the world taken by a camera gives significant information about where the imaged objects are. However, one piece of information that is typically not computable (without prior knowledge of the imaged object sizes) is the distance from the camera to any point in the scene. Thus, we have a bit more work to do if we want to re-construct a full 3D model of the scene in front of the camera. One approach is to simultaneously take pictures from two cameras with the same orientation but separated by a fixed distance. Because the views from each camera are different, it becomes possible to determine the distance to scene points by triangulation. Essentially, if we can identify a pair of pixels that image the same 3D point, one in the left camera image and the other in the right image, then the 3D coordinates of the point can be calculated as the intersection of light rays from that point to each of the pixels. The lower figure at right shows a rock on the surface of Mars, as imaged by a stereo pair on one of the Mars Exploration Rovers. Both the original (typically left camera) intensity image and a false-color “elevation map” image are shown. The elevation map is calculated by recovering the 3D coordinates of scene points for as many pixels in the left image as can be matched to pixels in the right image, and then colored according to height in a vertical coordinate frame.
 |
| [Christopher Wright] |
Cameras can produce a lot of information, especially when producing images at video rates (typically around 30 new images per second). One class of techniques for managing this volume of data is to first run an algorithm which finds salient or unique-looking visual features in each image. There are a variety of such algorithms in common use these days. We will study the fundamental concepts of how to make a mathematically precise statement about what actually makes a feature “salient”, and we will also learn about some of the key algorithms that are currently used in practice both to detect and to track features across video frames.
 |
| [Klein and Murray] |
This topic ties together four of the other topics: representing 3D poses, SLAM, stereo vision, and feature tracking. The idea is to perform SLAM using only a single camera. The camera can move around, and its 3D pose is tracked relative to a map that is also constantly being maintained of nearby feature points. Klein and Murray recently demonstrated an impressive real-time solution to this tough problem which they call Parallel Tracking and Mapping (PTAM). It performs the tracking and mapping as processes which run in parallel, and which can thus take advantage of parallel processing hardware when available. The image at right shows an application they developed called Ewok Rampage—an augmented reality game where 3D characters are virtually rendered into the video stream, correlated with actual objects in the world (and with the camera pose) using the map and tracking info from PTAM.
 |
| [Newcombe et al] |
Related to the ability to track the 3D pose of a camera in real time as it moves around in an unknown environment (as in monocular SLAM and PTAM) is the possibility to actually reconstruct a geometric model of that environment. This is not easy, but recently several amazing systems have been demonstrated that can build high quality 3D surface models. Some use only a single monocular camera, but an important new algorithm called Kinect Fusion uses Microsoft/PrimeSense Kinect. While the Kinect does capture a full 3D image, it does not by itself know its relative position as it may be moved around a scene. That information is needed in order to fuse together many individual Kinect scans to build high-quality scene models like the example shown here.
 |
| [Lamure, Michelucci 96] |
Given an initial rough sketch of ten circles and a triangle in the plane, as shown in the upper left, and the semantic constraints that (a) each circles must be tangent to its neighbors and (b) peripheral circles must be tangent to the triangle, how can we build an algorithm which will adjust the drawing so that the constraints are exactly met? (This example is due to Lamure and Michelucci.) This is an instance of a geometric constraint solving problem, which is encountered for example in the user interface of computer-aided design programs. Though this problem can be hard in general, we will study a few methods that work well in practical cases.
 |
| [Shigley, Uicker 80] |
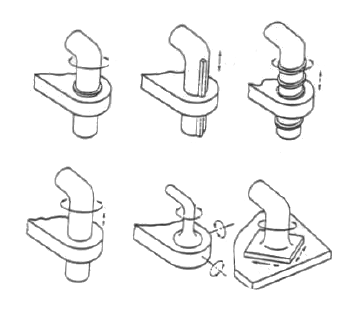
Adjacent sliding parts in a machine are typically designed to maintain a two-dimensional patch of contact throughout their motion, helping to ensure that pressure will not be concentrated at any single point. It has been known since the 19th century work of Reuleaux that there are at least six designs which achieve this: revolute, prismatic, helical, cylindrical, spherical, and planar joints, as shown here (starting in the upper left and moving across the top row, then across the bottom). But is this set complete? Are there any other types which maintain a 2D contact patch? The answer is no, a fact which was only proved in the last few decades. We will study how to model and simulate this important class of joints, known as lower pairs, and we will see how an analysis of their types is deeply connected with the study of continuous symmetry in 3D.
 |
| [Okada et al 01] |
The 3D world can be thought of, to some extent, as consisting of a collection of individual surface patches. These can be sampled (i.e. individual 3D points can be detected on them), by sensors including cameras and laser rangefinders. Typically the sampled points are not exact since there is possibly significant noise involved in the measurement process. How can an algorithm (a) figure out which sampled points belong to which surface, and (b) estimate models of the observed surfaces? This problem can actually be quite challenging, especially when we want answers quickly. Significant progress has been made for the case of planar patches, and research is ongoing for curved patches.
 |
| [Lam] |
At first, this problem may seem so simple that you would be surprised to know that entire books have been written on the subject. Given models of several 3D objects, typically represented as meshes of triangles covering their surfaces, and poses of each of those objects in space, how can we quickly calculate whether any of the objects is colliding (intersecting) any other? This is a very important question whenever we simulate motion of real-world objects, like the stacked boxes at right, because typically we will need to take special action to simulate the physics of collision when objects touch.
 |
| [Niklas Roy] |
In addition to tracking low-level geometric features, there has been significant research on a variety of topics related to tracking the location and the pose of human beings, using cameras and other types of sensor. The image here shows a “behind the scenes” view of an art installation that moves a small curtain based on the location of passers-by. Another very high-profile application is Microsoft’s project natal, which is now available as the Kinect peripheral for the Xbox 360. This device tracks the pose of multiple people for use in controlling games using a structured light technique, similar to stereo vision, to acquire 3D images.
 |
An accelerometer is a device which measures its own linear acceleration in 1, 2, or 3 orthogonal axes. Similarly, a gyroscope measures its own angular velocity in 1–3 axes, and a magnetometer measures the strength of any ambient magnetic field (such as that of the Earth), typically in 2 or 3 axes. Sensor fusion algorithms, including the Kalman Filter which is also used for SLAM, can be applied to combine raw data from these sensors to continuosly estimate an object’s position and orientation. The Nintendo Wiimote contains a 3-axis accelerometer, and most modern smartphones contain a 2-axis magnetometer used as a compass.
For each topic we will read a selection of top research papers from the literature. Each paper will be presented by the professor or by students followed by round-table discussion. Required background material will also be presented by the professor.
In the first part of the term there will be 2—4 homework assignments that will span both analytical work and coding. In the second part of the term, each student will either write a term paper on a related topic of their choosing or develop a software project (possibly working in pairs). There will be no quizzes or exams. Grading will be based on your class participation (including presentation of at least one paper), homeworks, and your final paper or project.
The basic parameters of the course are summarized below. All of the information on this website is subject to change—hit the “reload” button when viewing each page to be sure you see the newest revision, and not an old version that might have been cached by your browser. The timestamp of the revision you’re viewing is always shown at the bottom of the page.
Email: vona@ccs.neu.edu (webpage)
Office: 248 WVH
Office Hours: 4–5pm Tue or by appointment
140 Richards 5:30–7:20pm Mon/Weds
There is one required text, which we will use for many but not all of the topics:
Bradsky, Kaehler. Learning OpenCV: Computer Vision with the OpenCV Library. O'Reilly Media, 2008.
Individual readings from the research literature will also be assigned each week on the course schedule.
No specific prior experience with geometric computation is required for this course. We will cover each topic from the ground up. However, in order to participate,
you should be competent in multivariable calculus and linear algebra,
you should be able to analyze algorithms, and
you should know how to design and debug programs in an environment of your choice.
Please contact the instructor if you would like to take the course but are unsure if you meet these requirements.
This is a graduate-level course; participation from advanced undergraduates is also encouraged with permission from the instructor and the department.
