Introduction to Racket

Preliminary

To participate in this lab you will need to follow some basic first steps:

1. Groups of 2: For this laboratory, you need to form teams of two people. Each group will work on a single computer. Both people discuss the exercises and think about the problem in hand; only one of the two types the code. You should switch places with your partner in about the middle of the lab. Important Note: This pair work is only for this laboratory. Your first four problem sets will be done on an individual basis.

2. Run DrRacket: DrRacket will be our working Racket environment for this lab (and later for the CS 5010 problem sets). Find DrRacket in the Start menu and run it. Click "Choose Language..." either in the Language submenu in the menu bar or in the language selector in the bottom left corner of the DrRacket window and choose the "Beginning Student" language under "Teaching Languages / How to Design Programs".

When you do all of the above, you are ready for the lab.

During the lab, please try to do all the exercises through exercise 10. Go farther if you have time. There is no problem set this week, so you should spend this week doing more of the exercises to get used to working with Racket.

Expressions

Maybe the most fundamental building block in Racket (and other languages) is an expression. An expression is a piece of syntax that returns one result. An expression can be as simple as a single number

    5

or more complex as the calculation of the square root of a number

    (sqrt 5)

(Don't be alarmed if you don't understand the above syntax just yet.)

You can try typing the above examples in the bottom half (a.k.a. Interaction Window) of DrRacket. There you will see a prompt > and next to it you can type an expression. Whenever you write an expression next to the prompt and press enter, DrRacket will "evaluate" the expression and print the "result" in the line underneath.

    > 5
    5

    > (sqrt 5)
    2.23606797749979

In the next section we will see how we can use the interaction window of DrRacket as an advanced calculator.

Numbers, Booleans, and Arithmetic

As we mentioned above, some of the primitive expressions in Racket are numbers; positive and negative, integers and decimals

    > 17
    17

    > -10
    -10

    > 3.1415
    3.1415

Racket also has a set of arithmetic operators that work with numbers.

    ; + : Number Number -> Number
    ; Adds two numbers and returns the result

    ; - : Number Number -> Number
    ; Subtracts two numbers and returns the result

    ; * : Number Number -> Number
    ; Multiplies two numbers and returns the result

    ; / : Number Number -> Number
    ; Divides two numbers and returns the result

+, -, *, / are the names of the operators.

Number Number -> Number is the Contract for each of them. It guarantees that these operators take two numbers as arguments and return a number as a result. Knowing the contract of an operator is imperative in order to use it correctly!

Now let's see how we can apply these operators on some operands (a.k.a. arguments) and start doing something interesting with our Racket calculator.

To apply an operator on some operands we need a pair of parentheses that enclose both the operator and the operands, in order.

    > (+ 3 5)
    8

The operator is always the first thing in the parentheses, followed by the operands. Here + is the operator, 3 is the first operand, and 5 the second operand. The order of the operands is important:

    > (- 13 7)
    6

    > (- 7 13)
    -6

Whenever you see the "parentheses-notation" in Racket you should immediately recognize that it is the application of an operator to several operands, and you should be able to recognize that the first thing between the parentheses is the operator, the second thing is the first operand, the third is the second operand, etc.

So now we have a simple calculator where we can do one operation after the other. To calculate 3*2 + 5*3 we can type:

    > (* 3 2)
    6

    > (* 5 3)
    15

    > (+ 6 15)
    21

Remember that all of the above are expressions. Each one is being evaluated by DrRacket and a result is returned in its place. Having this in mind we can build more complex expressions, and make our calculator compute 3*2 + 5*3 writing just one big expression:

    > (+ (* 3 2) (* 5 3))
    21

Q: What is the order of evaluation in complex expressions?

When things get too complicated use indentation to make the expression more readable:

    > (+ (+ (- 20 5)
            (+ 10 4))
         (* (- 100 93)
            (* 3.5 
               (- 5 3))))
    78

We now know how to use Racket as a decent calculator to do arithmetic. But let's not stop there. Let's see how we can also do Logical calculations.

Racket has some more primitive expressions, the set of booleans:

    ; True
    > true
    true

    ; False
    > false
    false

It also provides operators that can be applied on booleans

    ; and : Boolean Boolean -> Boolean
    ; Logic conjunction

    ; or : Boolean Boolean -> Boolean
    ; Logic disjunction (Inclusive)

    ; not : Boolean -> Boolean
    ; Logic negation


    > (not false)
    true

    > (and true false)
    false

    > (or (and true
               (or true false))
          (or (not true)
              (not (and (not false)
                        true))))
    true

There are also operators that connect the "world" of numbers and the "world" of booleans. These operators perform tests on numeric data and return a boolean value. These are called predicates.

    ; = : Number Number -> Boolean
    ; Tests two numbers for equality

    ; < : Number Number -> Boolean
    ; Tests if the first operand is less than the second

    ; > : Number Number -> Boolean
    ; Tests if the first operand is greater than the second

    ; <= : Number Number -> Boolean
    ; Tests if the first operand is less or equal than the second

    ; >= : Number Number -> Boolean
    ; Tests if the first operand is greater or equal than the second

So for example:

    > (< 300.0001 300)
    false

    > (= (+ (* 3 50)
            (* 3 25))
         (* 3
            (+ 50 25)))
    true

Q: What will this return?

    > (< 3 (< 2 1))

Be careful of the contracts of operators to avoid these type errors.

Conditional

There are times that we need the value of an expression to change depending on some condition. Racket provides a construct to implement this kind of branching.

    (cond 
      [test-1 expr-1]
      [test-2 expr-2]
      [test-3 expr-3]
      ...
      [else expr-n])

The cond is a multi-branch conditional. Each clause has a test and an associated action. The first test that succeeds triggers its associated action. The final else clause is chosen if no other test succeeded.

For example:

      > (cond 
          [(< (sqrt 5) (/ 5 2)) true)
          (else false)])

Defining Functions

At this point our DrRacket calculator can do a great deal of things. It's almost like a scientific calculator, but we are not there just yet. It would be nice if we were able to define our own operators on numbers and booleans and extend the functionality of our calculator. Racket has a special syntax for doing just that:

    (define (op-name arg-1 arg-2 ...) expr)

With this syntax we can define a new operator called op-name that takes a number of arguments arg-1, arg-2, etc., and when applied evaluates the expression expr and returns the result. expr can refer to the arguments, to produce its resulting value. For example let's define the Boolean operation 'nand', using 'and' and 'not':

    ; nand : Boolean Boolean -> Boolean
    ; RETURNS the negative of the conjunction of the two given booleans.
    (define (nand x y)
      (not (and x y)))

We can use our addition just like any other operator:

    > (nand true true)
    false

Let's also define a function that computes the average of two numbers:

    ; average : Number Number -> Number
    ; RETURNS: the average of its arguments
    ; usage:
    ; (average 3 5)    =>  4
    ; (average -7 7)  =>  0

    (define (average x y)
      (/ (+ x y) 2))

Let's also define abs using cond:

    (define (abs x)
      (cond 
        [(< x 0) (- 0 x)]
        [else x]))

    ; f->c : Number -> Number
    ; GIVEN: a temperature in degrees Fahrenheit as an argument
    ; RETURNS: the equivalent temperature in degrees Celcius.
    ; Examples:
    ; (f->c 32)  => 0
    ; (f->c 100) => 37.77777777777778

    ; tip : NonNegNumber Number[0.0,1.0] -> Number
    ; GIVEN: the amount of the bill in dollars and the
    ; percentage of tip
    ; RETURNS: the amount of the tip in dollars.
    ; Examples:
    ; (tip 10 0.15)  => 1.5
    ; (tip 20 0.17)  => 3.4

Ex 6: One of the solutions of the quadratic equation is given by the formula:

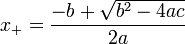
Write the contract, purpose statement, examples, and definition of a function quadratic-root that takes as arguments a, b, and c, and computes the root of the corresponding quadratic equation.

    ; circumference : Number -> Number
    ; GIVEN: the radius r of a circle 
    ; RETURNS: its circumference, using the formula 2 * pi * r.
    ; Examples:
    ; (circumference 1)  =>  6.283185307179586 
    ; (circumference 0)  =>  0

Complex Data Types: Structs

Number and Boolean are primitive data types in Racket. It is often useful to have more complex data types. Racket provides the possibility to just create those as we need them. The general scheme is:

    (define-struct data-type-name (field-1 field-2 ...))

The above code tells racket to introduce a type with a certain name that has certain named fields. Racket then creates some functions for us:

• make-data-type-name : T1 T2 ... -> Data-Type-Name

  This function takes as many arguments as there are fields in our type definition. Note that the contract here says T1 and T2 instead of Number or Boolean. That is because the types of the Fields can be different for every data type, i.e. you might want to create one where the first field is of type Number and another one where the first field is of type Boolean. You can even use a data type that you defined yourself!

• data-type-name? : Any -> Boolean

  This predicate takes anything as argument and returns true if that argument has the type that we just defined (i.e. if it was created by make-data-type-name (and of course false in any other case).

• data-type-name-field-1 : Data-Type-Name -> T1
data-type-name-field-2 : Data-Type-Name -> T2
  ...

  These functions can be used to extract the values that were given as arguments to make-data-type-name.

Let's see how that works in an example. The Racket student languages include a pre-defined data type called Posn. It represents a position in a two-dimensional plane, and is defined as follows:

    (define-struct posn (x y))

(Note that in this Lab write the type name with an upper-case first letter while we write names in definitions always in lower-case).

The above code lets Racket create the following functions:

• make-posn
• posn?
• posn-x
• posn-y

More on Struct-definitions

You should have done at least Ex11 and Ex13 before you continue here!

The contracts of make-posn and posn-x are

• make-posn : Number Number -> Posn
• posn-x : Posn -> Number

Racket also does not care what the values should represent and where. As long as it is a number, you can take an x-component of a Posn and use it somewhere where a percentage of something or a temperature in degress celsius is expected.

So racket does not generate the correct contracts of the posn-functions, nor do they appear out of thin air. We have to write down some information for other programs to know what contracts to follow. That is, somewhere we have to state the following:

• What actual types do the fields of the struct have (instead of T1, T2, etc.)?
• What do the fields represent (temperature (in degrees celsius or fahrenheit?)? distances (centimeters? meters? feet?)? ...)

The way we do this is a comment next to the struct-definition:

    (define-struct posn (x y))
    ;; A Posn is a (make-posn Number Number).
    ;; It represents a position on the screen.
    ;; Interpretation:
    ;;   x ... the x-coordinate on the screen (in pixels from the left).
    ;;   y ... the y-coordinate on the screen (in pixels from the top).

Here, the first line tells us what the types of the fields are (i.e. both x and y are Numbers) and the following tells us what the type in general and its fields in particular represent. Now it is easy for everyone to see that (make-posn true false) is not allowed and may lead to errors somewhere, and that x is neither degrees celsius nor meters nor feet.

Images

For this part, we will use an Image library that we will be using for the rest of the term. In order to use it, you best place the following code at the top of your file:

(require 2htdp/image)

In this class, we will work with images quite often. Here are the basic functions for drawing you will encounter:

    ;; bitmap : Path -> Image
    ;; Takes a path (as a string, e.g. "myfile.jpg") and loads that file as an image.
    
    ;; above : Image ... -> Image
    ;; Takes an arbirary number of images and places them above each other

    ;; beside : Image ... -> Image
    ;; Takes an arbirary number of images and places them beside each other

    ;; An OutlineMode is one of
    ;;  - "outline" ... only the shapes outline is drawn
    ;;  - "solid" ... the whole inside of the shape is filled

    ;; rectangle : Number Number OutlineMode Color -> Image
    ;; Creates an image of a rectangle with given width and height, drawing mode and color

    ;; circle : Number OutlineMode Color -> Image
    ;; Creates animage of a circle with given radius, drawing mode and color

    ;; text : String Number Color -> Image
    ;; Renders the given string in the given color with the given number as text size and
    ;; returns the resulting image

    ;; empty-scene : Number Number -> Image
    ;; Creates an empty white rectangle with given width an height
	
    ;; place-image : Image Number Number Image -> Image
    ;; Places the first image into the second image with its center at the given coordinates (x/y)

    ;; string-append : String ... -> String
    ;; Takes an arbitrary number of strings and concatenates them
    > (string-append "Hello " "World!")
    "Hello World!"

(define my-image (bitmap "[the file name of your image]"))

(above my-image my-image my-image)

    ;; rel-rec-sequence: Number Number -> Rectangle
    ;; Takes two numbers and returns a solid blue rectangle, where the first number is
    ;; the width of the rectangle, and the second number is the proportion of width
    ;; and height of the rectangle to be produced (i.e. height = width * proportion).

(define-struct person (first-name last-name age height weight))

Lists

Structs can already consist of more than one value, but very often we need to store an arbitrary amount of values. A fundamental part of programming in Racket lets us do just that: lists. In contrasts to the simple structs we have seen, there are two basic ways to create a list value. The first is rather self-explanatory:

    ;; empty : List
    ;; The empty list

    ;; cons: Any List -> List
    ;; Given some value and a list, creates a new list where the given value is the
    ;; first element and the given list is the rest of the new list.

    > (cons "Something" empty)
    (cons "Something" empty)

    > (cons "Something" (cons "Some other thing" empty))
    (cons "Something" (cons "Some other thing" empty))

Writing down all these constructors is a bit cumbersome, so here's a shorthand for creating lists:

    ;; list : Any ... -> List
    ;; Takes any number of values and returns a list of those values.
    ;; Example: (list 1 2 3 4 5) => (cons 1 (cons 2 (cons 3 (cons 4 (cons 5 empty)))))

    ;; list-fn : List -> ??
    ; (define (list-fn lst)
    ;   (cond
    ;     [(empty? lst) ...]
    ;     [else (... (first lst) (list-fn (rest lst)))]))

A interesting thing is the call to list-fn in the last line of list-fn. This is what we call recursion. There is a lot to be said about recursion later in the term, but for now we'll just use this technique to process lists.

Let us rather talk about what we do in this function: we get some list as an argument, and we know that there are two cases how that list could have been constructed: either using empty or using cons. Well, there has to be a result in any case, but if the list is empty, we cannot extract a value from it, so we have to replace the dots in the first case with a meaningful value in case the list is empty. If, on the other hand, there is a value and a rest, both of them may influence the final result of our computation. Therefore, we calculate the result of the computation of the rest of the list (which may be empty or have some more elements, but less than the list we were given) and then combine it with the first element. Let's look at an example:

    ;; sum : List -> Number
    ;; Returns the sum of the numbers in the given list
    ;; Examples: 
    ;; (sum empty) => 0
    ;; (sum (list 1)) => 1
    ;; (sum (list 1 2 3) => 6
    (define (sum lst)
      (cond
        [(empty? lst) 0]
        [else (+ (first lst) (sum (rest lst)))]))

Look what we inserted here: the sum of all the numbers in an empty list is clearly 0. And if we take the number that is first in a list and add it to the sum of all the numbers in the rest of the list, we clearly get the sum of all numbers in the list. We do not necessarily have to use any of the values in the list in every case:

    ;; list-length : List -> Number
    ;; Returns the length of the given list
    ;; Examples: 
    ;; (list-length empty) => 0
    ;; (list-length (list 1)) => 1
    ;; (list-length (list 1 2 3) => 3
    (define (list-length lst)
      (cond
        [(empty? lst) 0]
        [else (+ 1 (list-length (rest lst)))]))

Here, the length of an empty list is again clearly 0, and the length of a list where there is a first element and a rest must be 1 + the length of that rest.

Look at the following pieces of code. Is there anything wrong with either one or both of them?

    (list-length (list 1 5 "a" true 3))

    (sum (list 1 5 "a" true 3))

    ;; cons : Any List -> List

    ;; first : (NonEmpty-)List -> Any

    ;; cons : Number List-Of-Numbers -> List-Of-Numbers

    ;; first : (NonEmpty-)List-Of-Numbers -> Number

    ;; cons : Boolean List-Of-Booleans -> List-Of-Booleans

    ;; first : (NonEmpty-)List-Of-Booleans -> Boolean