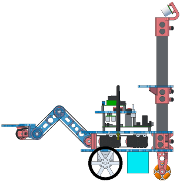
CS4610: Lecture 9 - Arm Kinematics
Arm Coordinate Frames
- Recall from Lecture 3 that we defined a world coordinate frame (w in the figure below) that is fixed to the environment, with standard basis
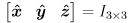 and origin
and origin 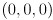 . The
. The 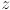 axis of world frame points up from the ground, and we normally draw the
axis of world frame points up from the ground, and we normally draw the 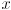 axis pointing right and the
axis pointing right and the 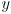 axis pointing up.
axis pointing up. - We also defined a robot frame (r in the figure below) that moves with the robot. It has basis
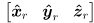 and origin
and origin 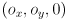 at the point on the ground midway between the two wheel contact points. (The basis and origin vectors of robot frame are expressed in world frame coordinates.)
at the point on the ground midway between the two wheel contact points. (The basis and origin vectors of robot frame are expressed in world frame coordinates.) 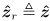 (i.e. the
(i.e. the 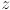 axis of robot frame also points up from the ground),
axis of robot frame also points up from the ground), 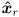 always points directly forward on the robot, and
always points directly forward on the robot, and 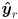 always points to the robot’s left.
always points to the robot’s left. 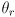 is the CCW positive angle from
is the CCW positive angle from 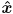 to
to 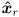 (i.e. from the world frame
(i.e. from the world frame 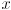 axis direction to the robot frame
axis direction to the robot frame 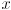 axis direction).
axis direction). - We now define several coordinate frames on the arm (see figure below):
- Frame 0 is attached to link 0 on the arm, the initial link that is rotated by the arm shoulder joint. The
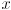 axis of frame 0 points down link 0; the
axis of frame 0 points down link 0; the 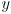 axis points to robot left, and the
axis points to robot left, and the 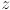 axis points “up” on link 0. The origin of frame 0 is the point where the arm shoulder rotation axis intersects the
axis points “up” on link 0. The origin of frame 0 is the point where the arm shoulder rotation axis intersects the 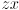 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 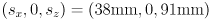 in robot frame.
in robot frame. - Frame 1 is attached to link 1 on the arm, the second link that is rotated by the arm elbow joint. The
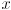 axis of frame 1 points down link 1; the
axis of frame 1 points down link 1; the 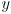 axis points to robot left, and the
axis points to robot left, and the 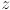 axis points “up” on link 1. The origin of frame 1 is the point where the arm elbow rotation axis intersects the
axis points “up” on link 1. The origin of frame 1 is the point where the arm elbow rotation axis intersects the 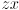 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 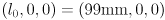 in frame 0.
in frame 0. - Frame 2 is attached to link 2 on the arm, the third link that is rotated by the arm wrist joint. This is also the link that carries the gripper. The
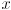 axis of frame 2 points down link 2; the
axis of frame 2 points down link 2; the 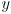 axis points to robot left, and the
axis points to robot left, and the 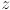 axis points “up” on link 2. The origin of frame 2 is the point where the arm wrist rotation axis intersects the
axis points “up” on link 2. The origin of frame 2 is the point where the arm wrist rotation axis intersects the 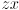 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 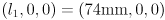 in frame 1.
in frame 1. - Frame g (gripper frame) is also attached to link 2; it models the point where an object could be gripped. It is co-oriented with frame 2, and its origin is the center of the circular notch between the gripper fingers, which is at the fixed location
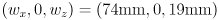 in frame 2.
in frame 2.
- The arm joint angles are
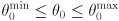 : the CCW positive angle from the direction of
: the CCW positive angle from the direction of  to
to 
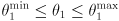 : the CCW positive angle from the direction of
: the CCW positive angle from the direction of 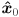 to
to 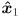
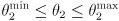 : the CCW positive angle from the direction of
: the CCW positive angle from the direction of 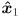 to
to 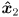 .
. - Positive values of each rotate the arm down (i.e. these are right-hand-rule rotations about the corresponding
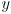 axes).
axes). - The ranges of motion are
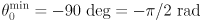 ,
, 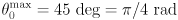
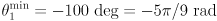 ,
, 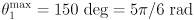
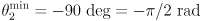 ,
, 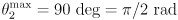 .
. - The figure shows the arm in home pose which has
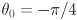 ,
, 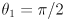 ,
, 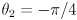 , and the gripper closed.
, and the gripper closed. - We also define a calibration pose where the arm is pointing straight forward, i.e.
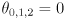 and the gripper is closed.
and the gripper is closed.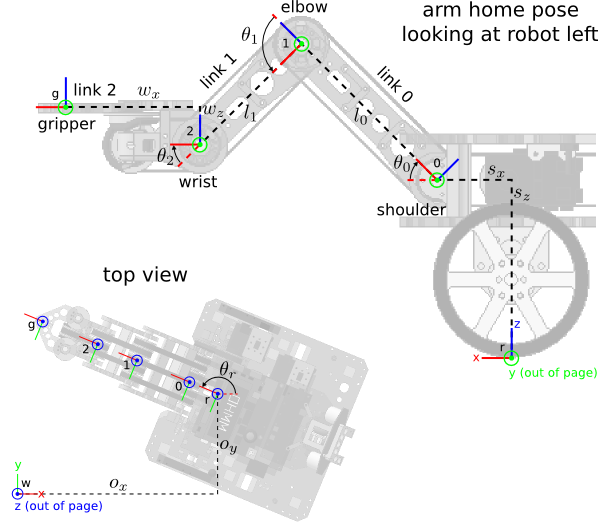
Forward Kinematics
- In Lecture 3 we also developed the forward position kinematics of the robot mobility, including a mathematical function with inputs
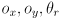 (the robot pose) and output
(the robot pose) and output 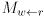 , a
, a 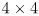 homogenous transformation matrix taking coordinates in robot frame to world frame.
homogenous transformation matrix taking coordinates in robot frame to world frame. - We can restate this function using two components:
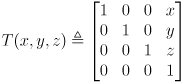 is a pure translation transform
is a pure translation transform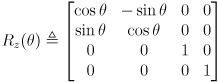 is a pure rotation about the
is a pure rotation about the 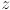 axis
axis
- Then
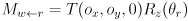 .
. - Remember, transforms compose from right to left. Given a 3D point
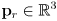 in robot frame, transform it to world frame
in robot frame, transform it to world frame 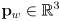 by appending an extra 1 and then left-multiply by
by appending an extra 1 and then left-multiply by 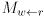 :
: 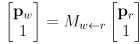
- We now extend this function to include the arm; the inputs will be
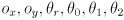 , and the output will be
, and the output will be 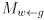 , a
, a 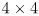 homogenous transformation matrix taking gripper frame to world frame.
homogenous transformation matrix taking gripper frame to world frame. - Defining
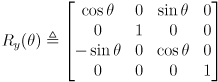 as a pure rotation about the
as a pure rotation about the 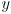 axis, continue the composition to include transforms all the way from gripper frame to world frame:
axis, continue the composition to include transforms all the way from gripper frame to world frame:
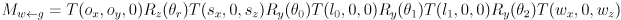
- Using abbreviations
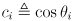 and
and 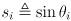 , and observing that the product of a pure translation and a pure rotation (in that order) is given simply by copying the upper left
, and observing that the product of a pure translation and a pure rotation (in that order) is given simply by copying the upper left  submatrix of the rotation and the upper right
submatrix of the rotation and the upper right  submatrix of the translation,
submatrix of the translation,
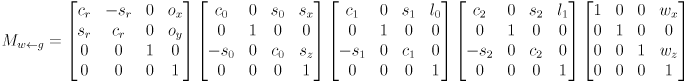
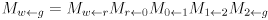
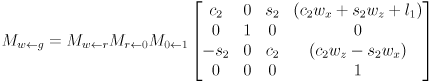
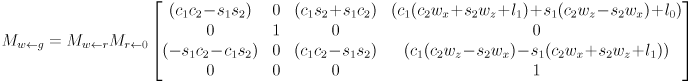
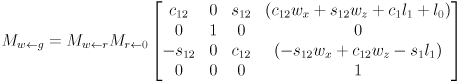 ,
, 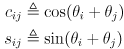
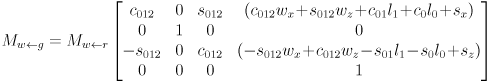 ,
, 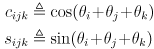
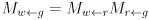
- This shows that the transform taking gripper frame to robot frame is the product of a pure translation and a pure rotation:
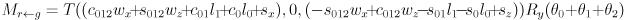
- In other words,
- the orientation of the gripper in the robot frame
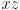 plane is
plane is 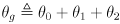 , i.e. the CCW positive angle from
, i.e. the CCW positive angle from 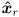 to
to 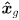 is the sum of the joint angles
is the sum of the joint angles - the gripper location in robot frame (the grip point) is
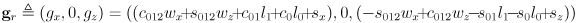
- in this case, both of these results could have been found directly using only basic trigonometry (in fact the derivation is very easy)
- but the transform composition formalism with homogenous transformation matrices works the same way for a very broad class of kinematic chains, not just this particular gripper, and it is efficient
Analytic Inverse Kinematics
- Just as inverse position kinematics was very useful for robot mobility, it will also be useful for the arm.
- Conceptually, we would like to literally invert the forward kinematic function.
- Recall that for robot mobility, this meant finding some drive trajectory that would bring the robot to a desired pose
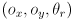 .
. - For the arm, we can define the inverse kinematic problem as finding a set of joint angles
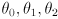 that put the gripper at a desired location
that put the gripper at a desired location 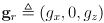 and orientation
and orientation 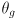 in the robot frame
in the robot frame 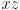 plane.
plane. - Later, we’ll show a simple extension that also uses turn-in-place wheel motions to allow the arm to reach a 3D volume in world frame.
- We’ll make one simplification: we will only solve a version of the problem where
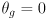 . That is, we will solve a restricted version of the arm IK problem where the gripper is always held parallel to the ground. This simplifies the math somewhat while still demonstrating the essence of IK. Also, it’s not too much of a compromise in many practical grasping tasks.
. That is, we will solve a restricted version of the arm IK problem where the gripper is always held parallel to the ground. This simplifies the math somewhat while still demonstrating the essence of IK. Also, it’s not too much of a compromise in many practical grasping tasks. - Inverse kinematics is a well-studied area. There are a number of approaches; two common ones are analytic (or closed form) IK and numeric (or iterative optimization) IK. We’ll first demonstrate an analytic IK solution for our arm; later we’ll re-solve the problem using the numeric approach.
- The basic idea of analytic IK is to try to algebraically invert the forward kinematics equations. When this is possible (and it is not always possible), the approach has several key properites:
- Once the IK equations are found (on paper), they can be coded up, and at runtime their solution(s) can be found (by definition) in constant time. So analytic IK is usually fast.
- Note carefully: there can be more than one solution. For example, in our version of the problem, the elbow could “kink” up or down.
- Unreachable targets are also identified in constant time.
- Here’s one way to solve our version of the IK problem with an analytic approach:
- First, since
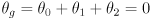 , we can immediately derive
, we can immediately derive
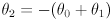 (1)
(1)
- The same fact implies
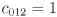 and
and 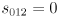 , which lets us simplify
, which lets us simplify
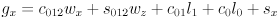
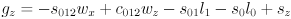
to
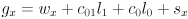
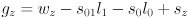
- Now expand the trig identities for angle sums
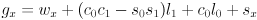 (2)
(2)
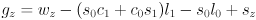 (3)
(3)
- and add the two identities
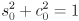 (4)
(4)
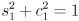 (5)
(5)
- Tecnically (2–5) are a system of 4 equations in 4 unknowns (
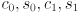 ), so we should be able to solve for all unknowns.
), so we should be able to solve for all unknowns. - This is a little tricky unless we apply some geometric insight. Define the reach triangle with vertices given by the origins of frames 0, 1, and 2 (i.e. the intersections of the shoulder, elbow, and wrist rotation axes with the vertical
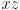 plane in robot frame). Two of the triangle side lengths are
plane in robot frame). Two of the triangle side lengths are 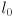 and
and 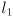 ; the angle between those two sides is
; the angle between those two sides is  . Defining the reach vector as
. Defining the reach vector as
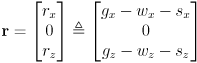 , the third triangle side has length
, the third triangle side has length
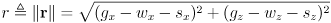 (6)
(6)
- Apply the cosine angle difference identity and the law of cosines to solve for
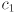 :
:
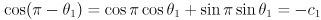 (7)
(7)
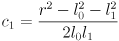 (8)
(8)
- If
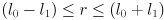 then (8) implies
then (8) implies 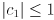 , but otherwise the given target is unreachable.
, but otherwise the given target is unreachable. - Assuming the target is reachable, use (5) to find
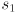 , taking the positive branch of the square root to make the arm “kink up”, i.e. to find a solution with
, taking the positive branch of the square root to make the arm “kink up”, i.e. to find a solution with  :
:
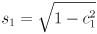 (9)
(9)
- Together, (8–9) determine
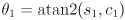 . (10)
. (10)
- The target is unreachable if
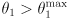 , otherwise continue.
, otherwise continue. - The final job is to calculate
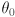 . It will be the difference of the orientation
. It will be the difference of the orientation
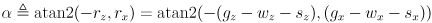 (11)
(11)
of the reach vector and the angle 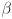 in the reach triangle between the sides with lengths
in the reach triangle between the sides with lengths 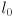 and
and 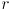 :
:
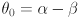 (12)
(12)
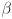 can be found by another application of the law of cosines:
can be found by another application of the law of cosines:
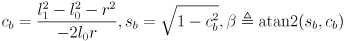 . (13)
. (13)
- The target is reachable if
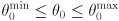 .
. - Finally, calculate
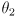 by (1); the target is reachable iff
by (1); the target is reachable iff 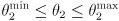 .
. - Summing up:
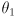 is calculated by (10), which depends on (6,8,9); then
is calculated by (10), which depends on (6,8,9); then 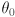 is calculated by (12) which depends on (6,11,13); and finally
is calculated by (12) which depends on (6,11,13); and finally 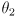 is given by (1).
is given by (1).
- This approach can be extended to include a “yaw” rotation by using the wheels to turn in place, which allows the arm to reach a 3D volume in world frame.
- Let the 3D target location for the gripper be
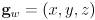 in world frame, and assume that the robot reference point is at the world frame origin.
in world frame, and assume that the robot reference point is at the world frame origin. - Calculate the yaw angle
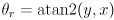 .
. - Transform
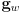 to
to 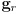 with the robot at orientation
with the robot at orientation 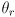 :
:
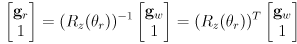
- This boils down to
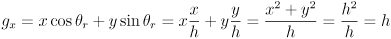
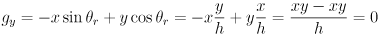

where 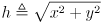 is the distance from robot frame origin to the projection of the grip point on the ground plane, and
is the distance from robot frame origin to the projection of the grip point on the ground plane, and 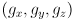 are the coordinates of the grip point in robot frame.
are the coordinates of the grip point in robot frame. - Continue as above with the target
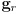 in the robot frame
in the robot frame 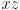 plane.
plane.
Numeric Inverse Kinematics
TBD
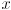 axis of frame 0 points down link 0; the
axis of frame 0 points down link 0; the 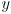 axis points to robot left, and the
axis points to robot left, and the 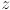 axis points “up” on link 0. The origin of frame 0 is the point where the arm shoulder rotation axis intersects the
axis points “up” on link 0. The origin of frame 0 is the point where the arm shoulder rotation axis intersects the 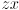 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 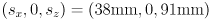 in robot frame.
in robot frame.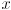 axis of frame 1 points down link 1; the
axis of frame 1 points down link 1; the 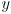 axis points to robot left, and the
axis points to robot left, and the 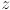 axis points “up” on link 1. The origin of frame 1 is the point where the arm elbow rotation axis intersects the
axis points “up” on link 1. The origin of frame 1 is the point where the arm elbow rotation axis intersects the 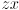 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 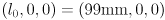 in frame 0.
in frame 0.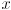 axis of frame 2 points down link 2; the
axis of frame 2 points down link 2; the 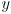 axis points to robot left, and the
axis points to robot left, and the 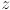 axis points “up” on link 2. The origin of frame 2 is the point where the arm wrist rotation axis intersects the
axis points “up” on link 2. The origin of frame 2 is the point where the arm wrist rotation axis intersects the 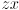 plane of robot frame, which is at the fixed location
plane of robot frame, which is at the fixed location 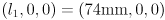 in frame 1.
in frame 1.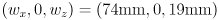 in frame 2.
in frame 2.
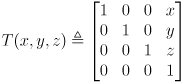 is a pure translation transform
is a pure translation transform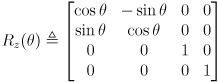 is a pure rotation about the
is a pure rotation about the 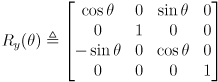 as a pure rotation about the
as a pure rotation about the 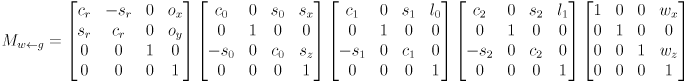
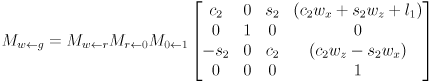
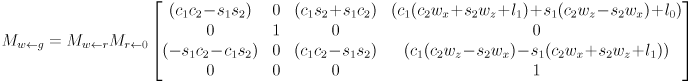
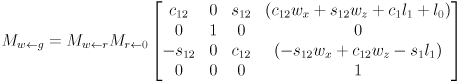 ,
, 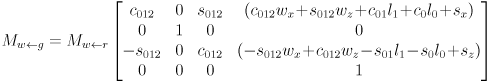 ,
, 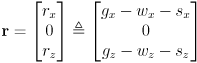 , the third triangle side has length
, the third triangle side has length