CS-2510 Assignment 1

Due: Thursday, September 15th @ 10:00 pm

Purpose:

This problem set is a review of CS 2500 concepts (data/function definitions, recursion, loops, and accummulators) in Racket. The HtDP book is available online.

Your solutions should be runnable in DrRacket using the HtDP Advanced Student language, and should be fully tested using check-expect.



Practice Problems:

Solve 31.3.3 and 31.3.4 in HtDP: For each problem, produce three different versions of the requested function using:
  1. The design recipe (structural recursion),
  2. An accumulator, and
  3. One of the loops: foldl or foldr (your choice).
Name the different functions appropriately (e.g., how-many, how-many-acc, how-many-fold)

Programming Problem 1:

Remember Racket structures? The DrRacket Student Languages have a built-in 2D position structure (Posn), You should also rember that the languages (and structure definitions in general) define some useful functions for posns: a constructor, predicate, and accessors. For example: 

     ;; Make a new Posn
     (define a-posn (make-posn 15 7))

     ;; Get its 'x' component
     (check-expect (posn-x a-posn) 15)

  1. Make a few Posn examples, and write a data-definition for a [listof Posn]. Make some examples of lists of Posns.
  2. Design a function just-xes that returns a list of all the 'x' components of a list of Posns. Remember that design means more than just writing the function. Follow the recipe!
  3. Design the same function (with a new name) using the Racket loop function map

  4. Design a function absolute->relative that calculates relative Posns for each of the list elements, starting at (0,0). In otherwords, return a new list of Posns that are adjusted so that they represent the change in position from the previous Posn in the list. Hint: think accumulator... what do you need to remember from earlier in the list?

    Here are a few tests... 

         ;; Basic Test...
     (check-expect (absolute->relative '()) '())
     ;; One Posn
     (check-expect (absolute->relative (list (make-posn 4 5)))
                   (list (make-posn 4 5)))
     ;; Two Posns in the same place
     (check-expect (absolute->relative (list (make-posn 4 5) (make-posn 4 5)))
                   (list (make-posn 4 5) (make-posn 0 0)))

     ;; A bunch of Posns...
     (check-expect (absolute->relative (list (make-posn 1 6) (make-posn 20 13)
                                             (make-posn 5 15) (make-posn 15 5)
                                             (make-posn 20 7)))
                   (list (make-posn 1 6) (make-posn 19 7)
                         (make-posn -15 2) (make-posn 10 -10)
                         (make-posn 5 2)))

  5. Design a function, say relative->absolute, that converts a list of 'relative' Posns into a list of 'absolute' Posns (again, starting at (0,0)).

    Note: The two functions you've designed should have no effect when applied in composition: 

         (define a-lop (list (make-posn 5 7) (make-posn 14 13)))
     (check-expect (relative->absolute (absolute->relative a-lop)) a-lop)

Programming Problem 2:

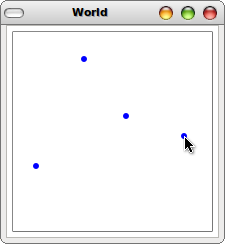
Consider/study the program below... well, paste the program into DrRacket and run it to see what it does. See the bottom of the page for a few screen shots on my computer. 
     (require 2htdp/image)
     (require 2htdp/universe)
     
     ;; Width and Height, and our base Scene
     (define WIDTH 200)
     (define HEIGHT 200)
     (define BASE-SCENE (empty-scene WIDTH HEIGHT))
     
     ;; A World is a [listof Posn]
     
     ;; put-dot : Scene Posn -> Scene
     ;; Put a single Dot into the Scene at the given Posn
     (define (put-dot scn p)
       (place-image (circle 3 'solid 'blue)
                    (posn-x p) (posn-y p)
                    scn))
     
     ;; draw-dots : World -> Scene
     ;; Draw the dots of the World (a list of Posn)
     (define (draw-dots ps)
       (cond [(empty? ps) BASE-SCENE]
             [else (put-dot (draw-dots (rest ps)) (first ps))]))
     
     ;; mouse : World Number Number Symbol -> World
     ;; Add a new Posn to the World if the mouse was clicked
     (define (mouse w x y what)
       (cond [(string=? what "button-down")
              (cons (make-posn x y) w)]
             [else w]))
     
     ;; Run the program...
     (big-bang '()
               (on-draw draw-dots)
               (on-mouse mouse))
Make the following additions to the program by completing the following functions:
  1. Transform draw-dots into accumulator style and call the new function draw-dots-acc. What does your function accumulate?
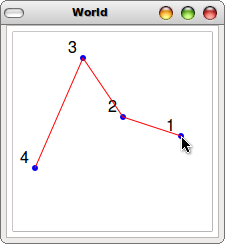
  2. Design the function draw-lines, in accumulator style that draws lines between the dots. Hint: you'll also want to pass the previous point's coordinates (in addition to the Scene accumulator) when you make your recursive call. See Image (2) for an example.
  3. Finally, design the function draw-num-lines that draws lines between and a number/label on each of the dots. See Image (3) for an example. Hint: you need to add one more accumulator. Don't worry if your numbers change as you add points... but feel free to fix it if you want.
Image (1) Image (2) Image (3)